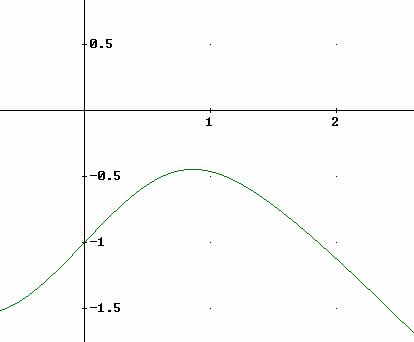
Problema 378.

Caracteritzeu pels seus angles tot triangle que virifique la relació tal que i r el radi de la circumferència inscrita.

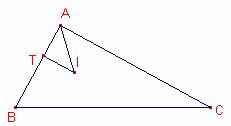
Solució de Ricard Peiró:

.

.

Resolent l’equació en r:

(*)

(*)

En qualsevol triangle , , .

Suposem que .

Si . La qual cosa és una contradicció.

Vegem que si el triangle és rectangle A. aleshores compleix les hipòtesis del problema.

Si un triangle és rectangle , , on .

.

Aleshores el problema sempre té almenys una solució, el triangle rectangle de catets b, c.

Suposem que el triangle és isòsceles

Sense restar generalització podem suposar que .

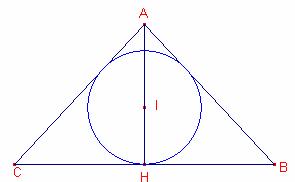Aleshores,

(1)

Siga altura del triangle isòsceles.

Siga I l’incentre del triangle .

.

, .

Aplicant la fórmula de la tangent de l’angle meitat:

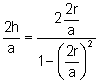, (2)

Aplicant el teorema de Pitàgores al triangle rectangle

(3)

Substituint l’expressió (2) en (3):

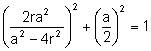. Simplificant:

(4)

Substituint (1) en (4).

Les solucions positives del qual són:

, ,

Si el triangle seria rectangle.

, el triangle seria acutangle, ja que .

no compleix les hipòtesis del problema.

Suposem que el triangle és escalè

Sense restar generalització podem suposar que .

Aplicant la fórmula de l’àrea del triangle:

Elevant al quadrat:

Com que sabem que és solució de l’equació podem factoritzar-la:

Les solucions de l’equació són:

el triangle seria rectangle A=90º

Siga

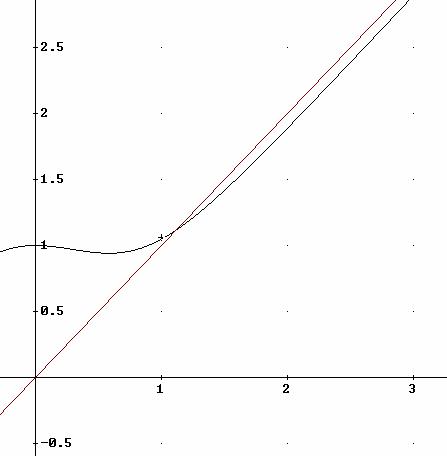
Considerem les funcions

La funció f(b) és estrictament creixent si b>1

Resolem

El valor aproximat és

Si aleshores que contradiu les hipòtesis del problema. En aquest cas el problema té una solució.

Si , el problema té dues solucions. Una solució és A=90º i l’altra el triangle és acutangle.

Si

si