Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 378

Caracterizar por sus ángulos a todo triángulo ABC,  que verifica la relación
tal que,  y r el radio de su círculo inscrito.

Romero, J.B. (2007): Comunicación personal.

Solución :

.

.

Resolviendo la ecuación en r:

(*)

(*)

En cualquier triángulo , , .

Supongamos que .

Si . Lo que es una contradicción.

Veamos que si el triángulo es rectángulo A. entonces cumple las hipótesis del problema.

Si un triángulo es rectángulo , , donde .

.

Entonces el problema siempre tiene por lo menos una solución, el triángulo rectángulo de catetos b, c.

Supongamos que el triángulo es isósceles

Sin quitar generalización podemos suponer que .

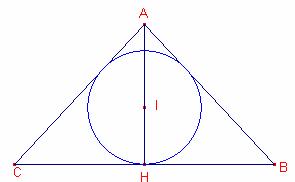Entonces,

(1)

Sea altura del triángulo isósceles.

Sea I el incentro del triángulo .

.

, .

Aplicando la fórmula de la tangente del ángulo mitad:

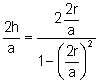, (2)

Aplicando el teorema de Pitágoras al triángulo rectángulo

(3)

Substituyendo l’expressió (2) en (3):

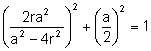. Simplificando:

(4)

Substituyendo (1) en (4).

Las soluciones positivas son:

, ,

Si el triángulo sería rectángulo.

, el triángulo sería acutángulo, ya que .

no cumple las hipótesis del problema.

Supongamos que el triángulo es escaleno

Sin quitar restar generalización podemos suponer que .

Aplicando la fórmula del área del triángulo:

Elevando al cuadrado:

Como sabemos que es solución de la ecuación podemos factorizarla:

Las soluciones de la ecuación son:

el triángulo sería rectángulo A=90º

Sea

Consideremos las funciones

La función f(b) es estrictamente creciente si b>1

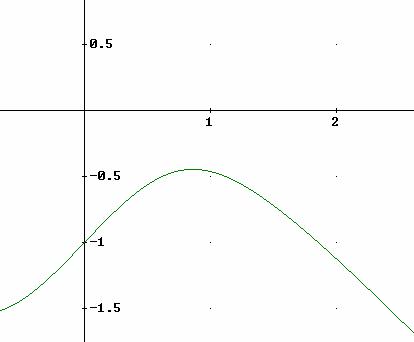
Resolvemos

El valor aproximado es

Si entonces que contradice las hipótesis del problema. En este caso el problema tiene una solución A=90º.

Si , el problema tiene dos soluciones. Una solución es A=90º y la otra el triángulo es acutángulo A<0.

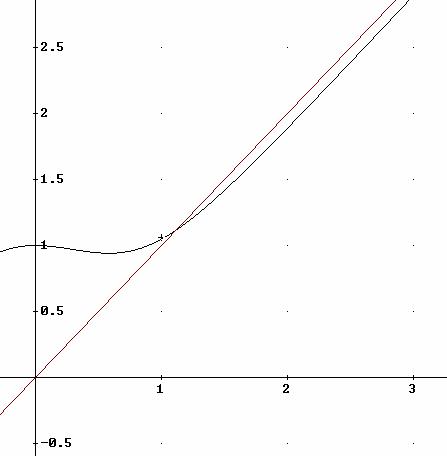
Si

si