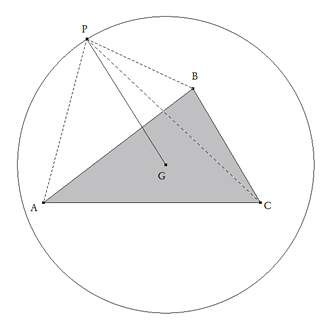
De Investigación. Propuesto por William Rodríguez Chamache. profesor de geometria de la "Academia integral class" Trujillo- Perú

Problema 380.

ABC: es un triángulo cualquiera. G: baricentro de ABC y sea P un punto en la circunferencia tiene como centro el punto G y como radio una longitud cualquiera. Demostrar que: PA2 + PB2+ PC2es constante.

Retali V, Biggiogero, G. (1936, 1979) "La geometria del triangolo " en "Enciclopedia delle matematiche elementari e complementari" Berzolari, Vivanti and Gigli , editores) Vol II , pp 175. El director agradece a Jeff Brooks y Marcello Brozolo del foro Hyacinthos, la referencia bibliográfica completa.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de abril de 2007)

DISCUSIÓN

Presentaremos dos soluciones, una solución con base en el cálculo y otra en la “fuerza bruta”.

PRIMERA SOLUCIÓN

Aplicaremos que la derivada de una función constante es la función nula.

SEGUNDA SOLUCIÓN

Aplicaremos simplemente las condiciones del enunciado.

Establecido ABC, queda unívocamente definido G. Por lo tanto cualquier punto P de un círculo con centro en G dependerá, en general, de un parámetro. Nosotros supondremos que este parámetro es t.

Utilizamos la siguiente notación

además, como P es un punto del círculo, tenemos la ecuación [1]

PRIMERA SOLUCIÓN

Derivando Ω respecto a t nos queda

Agrupamos y obtenemos

Teniendo ahora en cuenta la definición de G obtenemos la ecuación [2]

Retomando la ecuación [1] y derivando respecto a t obtenemos

resultado que introducimos en la ecuación [2] y obtenemos

LO QUE PRUEBA QUE LA EXPRESIÓN DEL ENUNCIADO ES CONSTANTE

SEGUNDA SOLUCIÓN

Expandamos la expresión de Ω

Si del ecuación [1] despejamos p₂ en función de p₁

y lo introducimos en la parte variable de la expansión de Ω

que queda como

que se simplifica en

y aún más en

que introducido en Ω acaba como

LO QUE PRUEBA QUE LA EXPRESIÓN DEL ENUNCIADO ES CONSTANTE