Problema 380

Siga un triangle qualsevol de baricentre G.

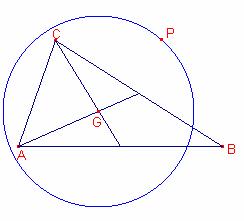
Siga P un punt en la circumferència de centre G i radi qualsevol. Demostreu que:

és constant.

Solució de Ricard Peiró:1:

Considerem el triangle amb les següents coordenades cartesianes:

, , .

El baricentre G del triangle té coordenades:

Considerem la circumferència de centre G i radi r, que té equació:

. Simplificant:

.

Considerem . Aquest punts satisfà l’equació de la circumferència:

(1)

=

Substituint l’expressió (1):

.

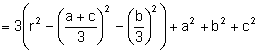Aleshores, és constant.

Solució 2:

Teorema: (Propietat vectorial del baricentre)

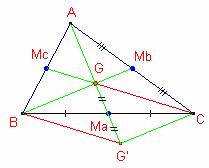Siga el triangle . Siga G el baricentre. Aleshores,

Demostració:

Siga G’ El simètric de G respecte del punt mig del costat a.

BG’CG és un paral·lelogram. Aleshores, (1)

Aplicant la propietat del baricentre: (2)

Substituint (1) i (2)

Aleshores,

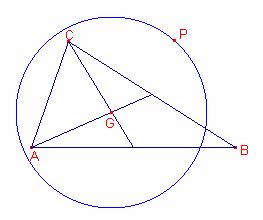Siga P un punt en la circumferència de centre G i radi r.

.

.

.

.

Aplicant la propietat del baricentre

.

Aleshores, és constant.