Problema 380

: es un triángulo cualquiera. G: baricentro de

Sea P un punto en la circunferencia tiene como centro el punto G y como radio una longitud cualquiera

Demostrar que: es constante.

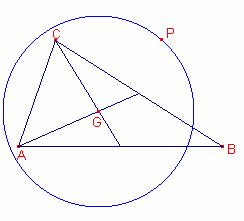Solución Solució de Ricard Peiró:1:

Consideremos el triángulo con las siguientes coordenadas cartesianas:

, , .

El baricentro G del triángulo tiene coordenadas:

Consideremos la circunferencia de centro G y radio r, que tiene ecuación:

. Simplificando:

.

Consideremos . Este punto satisface la ecuación de la circunferencia:

(1)

=

Substituyendo la expresión (1):

.

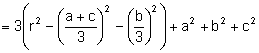Entonces, es constante.

Solución 2:

Teorema: (Propiedad vectorial del baricentro)

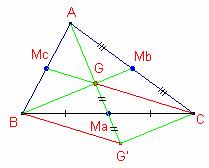Sea el triángulo . Sea G el baricentro. Entonces,

Demostración:

Sea G’ El simétrico de G respecto del punto medio del lado a.

BG’CG es un paralelogramo. Entonces, (1)

Aplicando la propiedad del baricentro: (2)

Substituyendo (1) y (2)

Entonces,

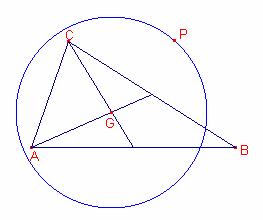Sea P un punto en la circunferencia de centro G y radio r.

.

.

.

.

Aplicando la propiedad del baricentro

.

Entonces, es constante.