De Investigación

Propuesto por William Rodríguez Chamache. profesor de geometria de la "Academia integral class" Trujillo- Perú

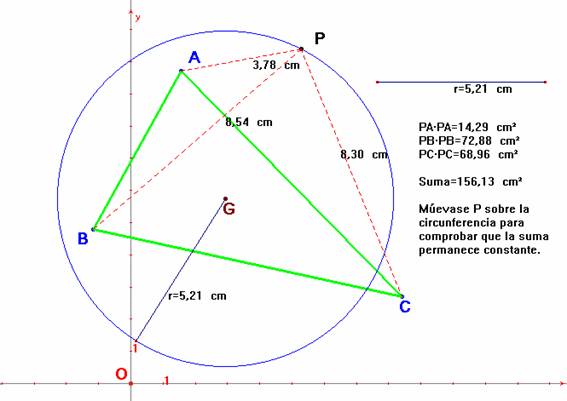
Problema 380.- ABC es un triángulo cualquiera. G: baricentro de ABC. Sea P un punto en la circunferencia tiene como centro el punto G y como radio una longitud cualquiera

Demostrar que: PA² + PB²+ PC² es constante.

Retali V, Biggiogero, G. (1936, 1979) "La geometria del triangolo " en "Enciclopedia delle matematiche elementari e complementari" Berzolari,
Vivanti and Gigli , editores) Vol II , pp 175.

El director agradece a Jeff Brooks y Marcello Brozolo del foro Hyacinthos, la referencia bibliográfica completa.

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca

Si ponemos coordenadas a los vértices del triángulo, A=(a₁,a₂), B=(b₁,b₂) y C=(c₁,c₂), el baricentro tiene coordenadas G=(g₁,g₂), donde 3·g₁= a₁ +b₁+ c₁ y 3·g₂= a₂ +b₂+ c₂. Un punto P(x, y) situado en una circunferencia de centro G y radio r tiene unas coordenadas paramétricas (las polares para esa circunferencia, 0≤a≤2p)

x= g₁ + r cos a

y= g₂ + r sen a

Hay calcular el cuadrado de la longitud de los vectores PA, PB y PC.

Tendremos PA² = (a₁– g₁–r cos a)²+(a₂ – g₂ – r sen a)² =

(a₁– g₁)²+(a₂ – g₂)²+r² –2· r cos a·(a₁–g₁)–2 r sen a·(a₂–g₂)=

=AG²+ r²–2· r cos a·(a₁–g₁)–2 r sen a·(a₂–g₂).

Con los otros vértices

PB²= BG²+ r²–2· r cos a·(b₁–g₁)–2 r sen a·(b₂–g₂),

PC²= CG²+ r²–2· r cos a·(c₁–g₁)–2 r sen a·(c₂–g₂).

Al sumar los tres términos, teniendo en cuenta que 3· g₁= a₁ +b₁+ c₁ y 3· g₂= a₂ +b₂+ c₂, los sumandos que tienen el seno y el coseno se anulan quedando finalmente

PA²+ PB²+ PC² = AG²+ BG²+ CG²+ 3r²

expresión que sólo depende del triángulo y del radio de la circunferencia.