Solución
de Francisco Javier García
Capitán|
11. Demostrar que en cualquier triángulo rectángulo
el punto de intersección de las mediatrices de los dos catetos
es el punto medio de la hipotenusa. |
|
Birkhoff, G. D. y Beatley, R. (1959)
Basic geometry. Chelsea P.C. New Cork.(p. 101)
|
Solución
de Francisco Javier García
Capitán
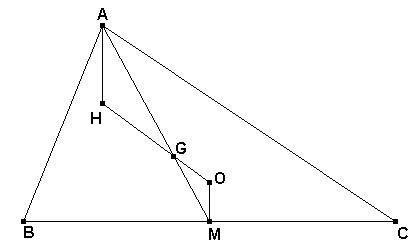
Usemos que el ortocentro H, el baricentro G y el circuncentro O de un triángulo ABC cualquiera están alineados (sobre la recta de Euler), siendo además HG:GO = 2:1.
Sea M punto medio del lado BC. Al ser paralelas las rectas AH y OM, tendremos que
AH = 2 OM.
A partir de aquí podemos resolver nuestro problema y su recíproco, ya que
O = M Û OM = 0 Û AH = 0 Û AB y AC son perpendiculares Û El triángulo ABC es rectángulo en A.