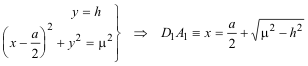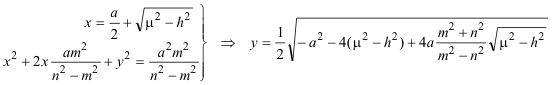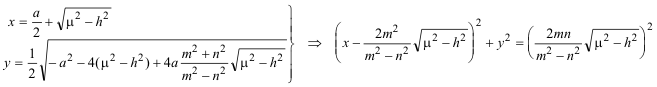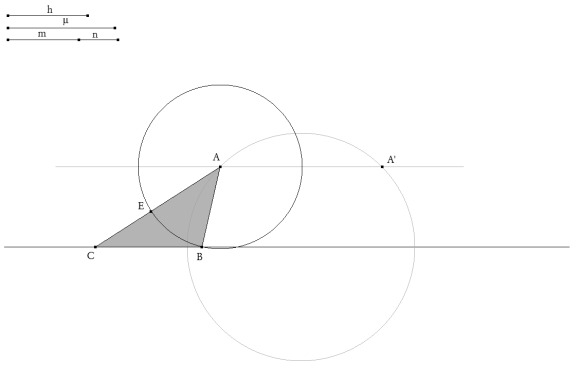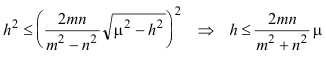De Investigación. Propuesto por Sergio Barrios Heyn, Ingeniero Civil, Paraguay

Problema 382 . Construir un triángulo conociendo las longitudes de la altura y la mediana relativa al lado a, y conociendo la relación de los lados b/c=m/n, siendo m y n segmentos de longitud conocida.

Examen Final de Geometría P y E,(1995) Profesores Ingenieros Darío Coronel y Pedro Echauri, Febrero Universidad Nacional de Asunción (Paraguay)

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 de abril de 2007)

PLANTEAMIENTO

El hecho de que tengamos la altura y la mediana nos proporciona dos lugares geométricos cuya intersección definiría el vértice A siempre que tuviésemos definidos B y C. Si eso fuera así, recordando que el lugar geométrico de los puntos, cuyas distancias a dos puntos dados (B y C) están en una proporción dada (m/n), es un círculo (Apolonio); este círculo debería contener también al vértice A.

La pega es que nosotros podemos fijar el vértice C; pero no el vértice B. Según fijemos B obtendremos distintos círculos de Apolonio que nos determinarán un nuevo lugar geométrico (que determinaremos) que junto con los dos anteriores (altura y mediana) nos fijarán la posición del vértice A y por tanto el triángulo solución ABC que responde al enunciado.

Para que la solución sea cómoda (regla y compás), el nuevo lugar geométrico debe ser una recta o un círculo; aunque CABRI, con su herramienta lugar, permite otros muchos y diversos lugares.

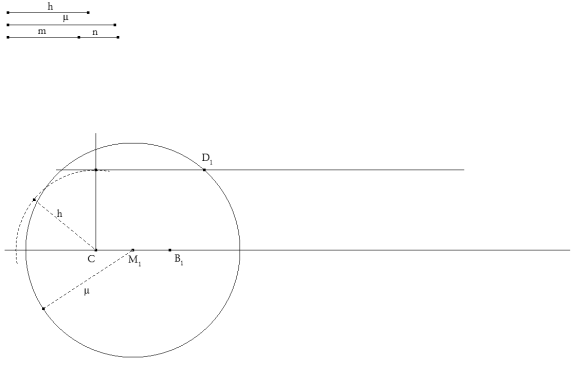
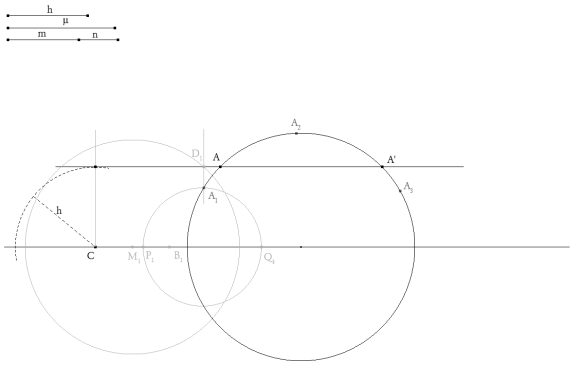
figura 1

Colocamos los datos del enunciado. Tomamos un punto cualquiera como vértice C. Una recta horizontal por C contendrá al lado BC; una paralela a esa recta y a distancia h (altura) deberá contener al vértice A.

Tomamos sobre la recta que contiene a BC un vértice variable B₁. Trazamos ahora M₁ punto medio de C y B₁

Con centro en M₁ trazamos el círculo de radio μ (mediana) que corta a la paralela anterior en D₁. Si B₁ fuera solución, D₁ sería A; pero en general no será así. Es por ello que determinaremos ahora el círculo de apolonio de C y B₁ con razón m/n.

figura 2

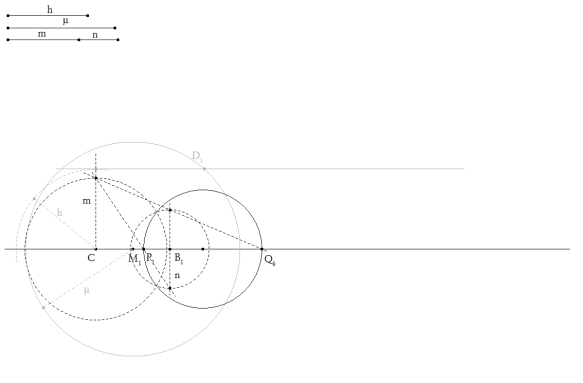
Para ello, círculo de centro C y radio m y círculo de centro B₁ y radio n (ver figura 2), uniendo los extremos de los diámetros de esos dos círculos perpendiculares a BC, obtenemos el diámetro del círculo de Apolonio P₁Q₁ y por tanto el círculo.

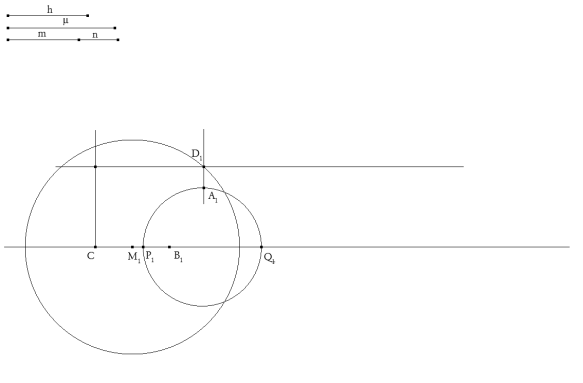
figura 3

Como era de suponer, el círculo de Apolonio hallado no pasa por D₁; pero corta a una perpendicular desde D₁ al lado BC en un punto A₁ que !!!si fuera el vértice buscado coincidiría con D₁¡¡¡.

Hallemos pues el lugar del punto A₁. Para ello, hacemos

y la ecuación de la recta D₁A₁es

Si P=(x, y) es un punto del círculo de Apolonio

El punto A₁ estará en la intersección de este círculo y la recta D₁A₁

y eliminado ahora el parámetro a entre x e y, nos queda

Lo que nos demuestra que es un círculo del que conocemos radio y círculo.

SOLUCIÓN

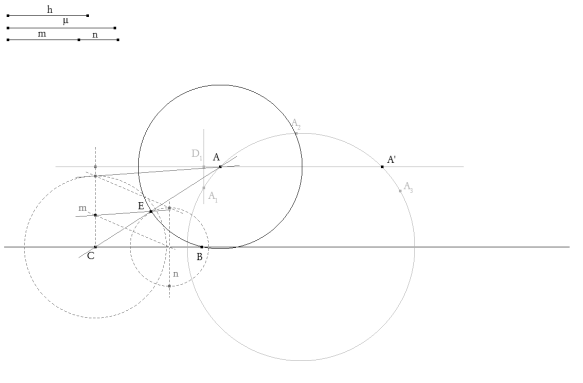
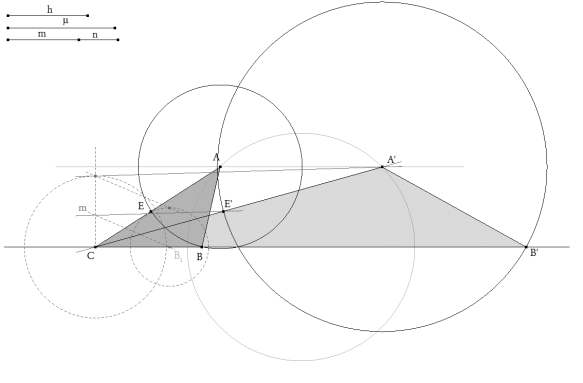
figura 4

Nosotros tenemos CABRI, por lo que tomando dos puntos más B₂ y B₃ podemos determinar A₂ y A₃ que junto con A₁ nos determinan el círculo buscado. Este círculo corta en A y A’ a la paralela de altura h sobre BC.

A es el vértice de la primera solución.

figura 5

Aprovechando los círculos de radio m y n usados para el círculo da Apolonio, determinamos

El círculo de centro A y radio AE corta al lado BC en B (la otra intersección no cumple con la mediana y por lo tanto no es solución).

figura 6

Obtenemos la primera solución ABC.

figura 7

Con A’ y procediendo de igual forma, obtenemos la segunda solución A’B’C (obsérvese que la segunda intersección coincide con la anterior que no es solución).

CONSTRUCCIÓN DINÁMICA

PUEDE DESPLAZAR LOS PUNTOS 1,2,3 (altura, mediana, m/n)

Figura 382Din.fig

José María Pedret 16/04/07CabriJava

DISCUSIÓN

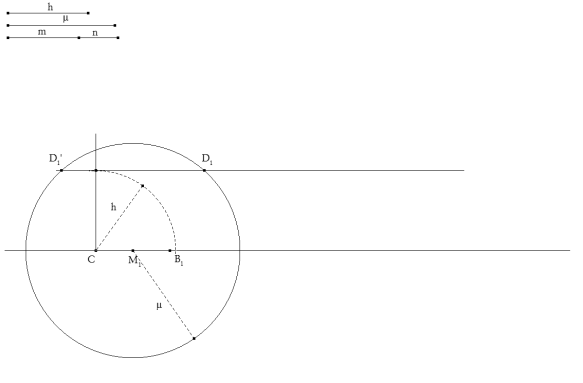
figura 8

Observando la figura 8 vemos que podemos obtener más soluciones si consideramos el segundo punto de intersección D₁’; pero para ello el círculo de Apolonio solución debería de cortar en ese lado y por lo tanto debería ser m/n<1.

Además, para que exista solución la altura debe ser menor o igual al radio del círculo hallado, de donde

de lo que se desprende la relación entre la altura y la mediana para que exista solución.