De Investigación. Propuesto por Sergio Barrios Heyn, Ingeniero Civil, Paraguay

Problema 382: Construir un triángulo conociendo las longitudes de la altura y la mediana relativa al lado a, y conociendo la relación de los lados b/c=m/n, siendo m y n segmentos de longitud conocida.

Examen Final de Geometría P y E,(1995) Profesores Ingenieros Darío Coronel y Pedro Echauri, Febrero Universidad Nacional de Asunción (Paraguay)

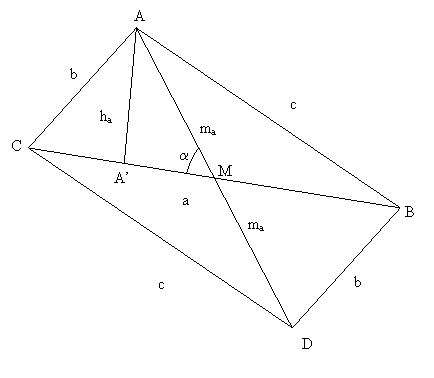
Solución 1, por Ing. Sergio Barrios Heyn

Suponiendo “construido” el triángulo ABC,

Se trazan paralelas a los lados AC y BC,

por los puntos B y C.

Dichas paralelas se cortan en D

ABDC, resulta un paralelogramo.

Los segmentos AC y DB, son iguales,

análogamente CD y AB.

Al trazar AD, se corta con BC en el punto M.

M es punto medio de las diagonales AD y BC.

AM, es la mediana m_a del triángulo ABC,

y de igual magnitud que MD.

Como se conoce la relación entre b y c, la misma puede ser

aplicada a los segmentos CA y CD, para construir el Círculo de Apolunio que determina el Lugar Geométrico del Punto C, tomando como base AD, que tiene una magnitud 2m_a

finalmente, dicho círculo se corta con la recta obtenida al construir el triángulo AA’M (rectángulo en A’), tomando como base el segmento AM.

Al conocer el punto C, se duplica CM a partir de M, para obtener B.