De Investigación. Propuesto por Sergio Barrios Heyn, Ingeniero Civil, Paraguay

Problema 382: Construir un triángulo conociendo las longitudes de la altura y la mediana relativa al lado a, y conociendo la relación de los lados b/c=m/n, siendo m y n segmentos de longitud conocida.

Examen Final de Geometría P y E,(1995) Profesores Ingenieros Darío Coronel y Pedro Echauri, Febrero Universidad Nacional de Asunción (Paraguay)

 

Solución 2, por Ing. Sergio Barrios Heyn

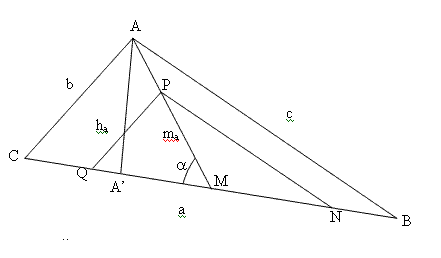
Suponiendo “construido” el triángulo ABC,  Siendo M el pie de la mediana m_a,

Tómese sobre la recta AM, un punto  cualquiera P.

Por P, trácense paralelas a los lados  AC y BC, dichas paralelas se cortarán a

la recta CB en los puntos Q y N.

Existe semejanza entre los triángulos CAB y QPN.

(puede explicarse en forma breve, a través de homotecia, con A o M) como centros

QP y PN están en la misma relación m/n dada.

D

Construcción

Constrúyase el triángulo AA’M (rectángulo en A’). Sobre A’M, tómese a cada lado de M, un punto equidistante de M. (valor arbitrario).

Llamando a esos puntos Q y N, se tiene la base para construir un círculo de apolunio, que corta a la recta AM en un punto P.

Trazando PQ y PN, se tiene un triángulo semejante al buscado.

Las paralelas por A, solucionan el resto