Problema 383

Sea ABC un triángulo rectángulo e isósceles, con AB=AC. Consideramos los puntos M y N en AB tales que AM=BN. Se traza desde A la perpendicular a CM que corta a BC en P. Si <APC=62º, calcular la medida del ángulo <BNP.

Solución Ricard Peiró:

Dado el triángulo rectángulo isósceles , , construimos el cuadrado ABDC.

Sea .

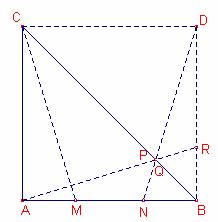Prolonguemos el segmento que corta el lado del cuadrado en R.

Los triángulos , son iguales y simétricos respecto de . Entonces se interesecten en el mismo punto de .

Entonces, .

Calculemos .

Si y .

Entonces, .