|
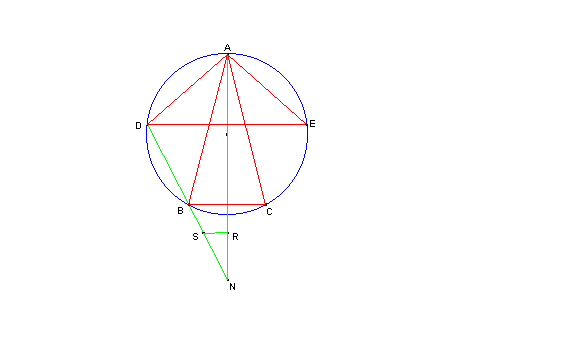
Problema 385 Inscribir en un círculo dado, de centro O y radio r, un triángulo isósceles del que se conoce la suma s de la base y de la altura. Discutir la existencia de soluciones según el valor de s respecto al radio r del círculo. Propuesto por Jose María Pedret. Solución de Mariano Nieto . Ingeniero de Minas, de Madrid. Sea AN = s, con un extremo A sobre la circunferencia de radio r y pasando por su centro O A partir de N construyamos el triángulo rectángulo en R, NRS, tal que NR = 2 RS. Prolonguemos el lado NS hasta que corte a la circunferencia en los puntos B y D, por los que trazaremos perpendiculares BC y DE a AN. Obtenemos así los triángulos ABC y ADE que cumplen la condición del problema. En el caso de que la recta NS fuese tangente al círculo tendríamos
una única solución y entonces |