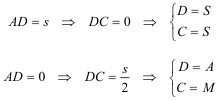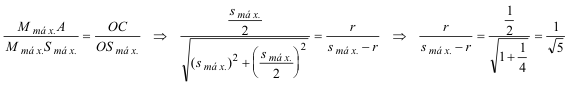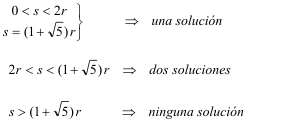De Investigación. Propuesto por José María Pedret. Ingeniero naval. (Esplugas de Llobregat, Barcelona).

Problema 385. Inscribir en un círculo dado, de centro O y radio r, un triángulo isósceles del que se conoce la suma s de la base y de la altura. Discutir la existencia de soluciones según el valor de s respecto al radio r del círculo.

Problème 105. Reynaud, Antoine-André-Louis (1771-1844). Théorèmes et problèmes de géométrie; suivis de la théorie des plans, et des préliminaires de la géométrie descriptive: comprenant la partie exigée pour l'admission à l'École polytechnique, 10e éd. Paris. 1838.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 de abril de 2007)

PLANTEAMIENTO

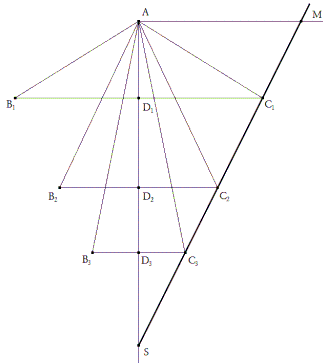
Para hallar un método de solución, en primer lugar prescindiremos del círculo y estudiaremos cual es el lugar geométrico de un vértice de la base de un triángulo isósceles que tiene fija la suma de la altura AD y la base BC.

relación lineal que nos indica que el lugar de dicho vértice es una recta.

Por un punto cualquiera que será el vértice A trazamos una recta AS con

figura 1

El lugar del vértice C es fácil de determinar pues

Por A trazamos una perpendicular a AS y sobre ella el punto M tal que

El lugar buscado es la semi-recta SM con origen en S.

SOLUCIÓN

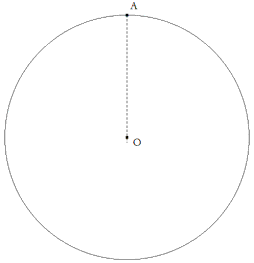
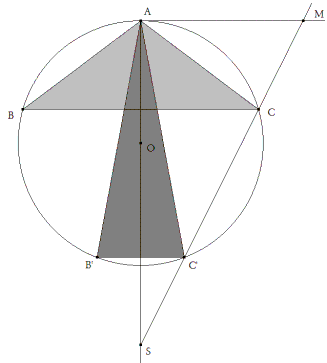
Sea el círculo dado de centro en O y radio

figura 2

Podemos ahora tomar AS sobre AO y trazar el lugar SM tal como hemos visto en el planteamiento.

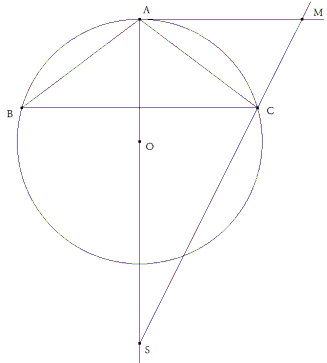
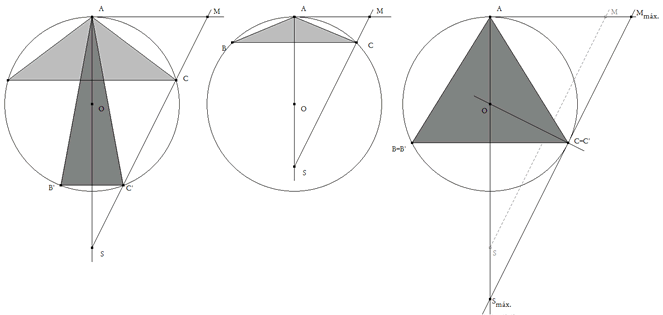
figura 3

como el triángulo debe ser inscrito al círculo, el vértice C se encontrará en la intersección del círculo con SM.

figura 4

El simétrico de C respecto AO nos proporciona el otro vértice B y ya podemos trazar el triángulo ABC.

figura 5

La segunda intersección C’ nos proporciona una segunda solución AB’C’.

CONSTRUCCIÓN DINÁMICA

PUEDE DESPLAZAR EL PUNTO O (radio del círculo) Y EL PUNTO S (suma)

Figure 385.fig

José María Pedret 16/04/07CabriJava

DISCUSIÓN

figura 6

Observando la figura central vemos que en el caso de que S sea interior al círculo, existe una sola solución.

Observando la figura de la izquierda vemos que si S es exterior al círculo existen dos soluciones. Las dos soluciones se convierten en una en el momento que SM es tangente al círculo.

Al tener los dos un ángulo recto y un ángulo en común, los triángulos [AS_máx.M_máx.] y [CS_máx.O] son semejantes y por tanto

y de aquí obtenemos

En conclusión si