De Investigación

Propuesto por José María Pedret. Ingeniero naval. (Esplugas de Llobregat, Barcelona),

Problema 385

Inscribir en un círculo dado, de centro O y radio r, un triángulo isósceles del que se conoce la suma s de la base y de la altura.

Discutir la existencia de soluciones según el valor de s respecto al radio r del círculo.

Problème 105. Reynaud, Antoine-André-Louis (1771-1844). Théorèmes et problèmes de géométrie; suivis de la théorie des plans, et des préliminaires de la géométrie descriptive: comprenant la partie exigée pour l'admission l'École polytechnique, 10e éd. Bachelier. Paris. 1838

Solución analítica de Ricard Peiró:

   

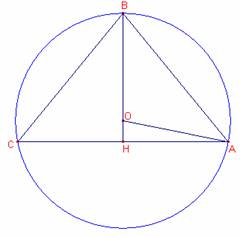
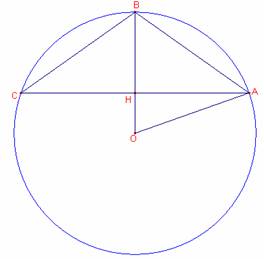
Sea , .

Sea .

Aplicando el teorema de los senos al triángulo .

. Entonces:

                            (1)

Aplicando razones trigonométricas al triángulo rectángulo :

. (en los dos casos). Entonces:

                       (2)

Sumando las expresiones (1) y (2):

.

Sea . Entonces, .

 

Resolvemos la ecuación: .

El problema tiene solución si  y  .

Resolviendo el sistema de inecuaciones:

Si , es decir si .

Si .

.

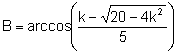
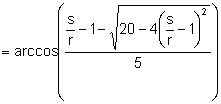Entonces, .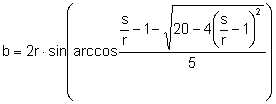

O bien:

.

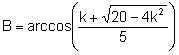
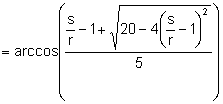Entonces, .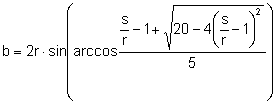

Con lo que tenemos determinado el triángulo isósceles. El problema tiene dos soluciones si .

Si .

.

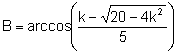
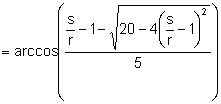Entonces, .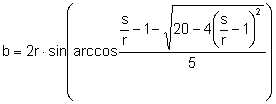

Con lo que tenemos determinado el triángulo isósceles. El problema tiene una solución si .

Si

.

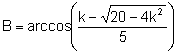
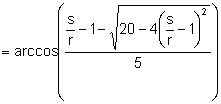Entonces, .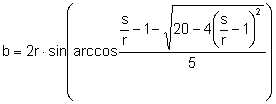

Con lo que tenemos determinado el triángulo isósceles. El problema tiene una solución si .