Para el aula
Problema 386
Triángulos y polígonos
47. ABC es un triángulo equilátero. Si D es el incentro, y trazamos las paralelas por D a AB y a AC, que cortarán a BC en P y R, demostrar que Q (Es P) y R triseccionan a BC.
Aref, M.N., Wernick,W. (1968): Problems &Solutions in Euclidean Geometry. Dover Publications, Inc, New York. (pag. 29)
Solución del director de la revista.
En primer lugar se debe aclarar que donde dice Q, es obviamente P
Sea ABC el triángulo, y D el incentro.
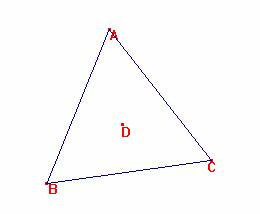
Tracemos las paralelas a AB y BC por D. Tracemos también la paralela a BC por D, y tracemos los segmentos que unen todas las intersecciones de las trazadas con los lados del triángulo original.
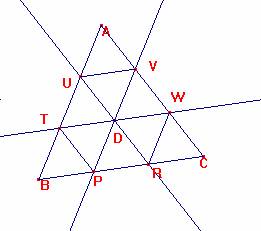
Se tienen así nueve triángulos equiláteros.
Luego BP=TP=DP=PR=DR=RW=RC, cqd.
Ricardo Barroso Campos
Didáctica de las Matemáticas
Universidad de Sevilla.