De Investigación
Propuesto por Juan Bosco Romero Márquez, profesor colaborador de
Problema 388
Sean O, O' los centros, y r, R los radios de las circunferencias inscrita y circunscrita de un triángulo ABC; Sean también A', B', C' los pies de las perpendiculares desde los vértices a los lados opuestos, I su intersección, y t el radio de la circunferencia inscrita en A'B'C'. Demostrar que
1) (OI)^2 = 2 r^2- 2Rt,
2) (O´I)^2 = R^2 - 4Rt.
Heal, W. E. (1886): The
Annals of Mathematics, Vol.2, No.2, (Feb.1886), pp. 43-47
RESOLUCION
de Frank Guiuseep
Coronado Idrogo,
Primera parte
Los triángulos rectángulos IPH y ONC sen semejantes luego: ![]()
Ahora sabemos que: ![]()
Finalmente en el triángulo: BOI aplicamos teorema de
Euclides.
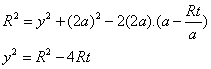
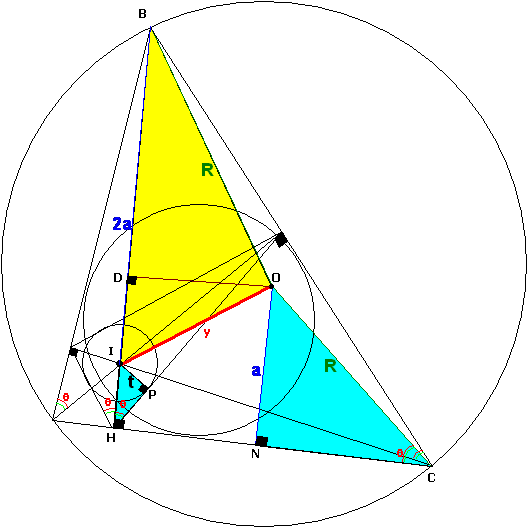
Segunda parte
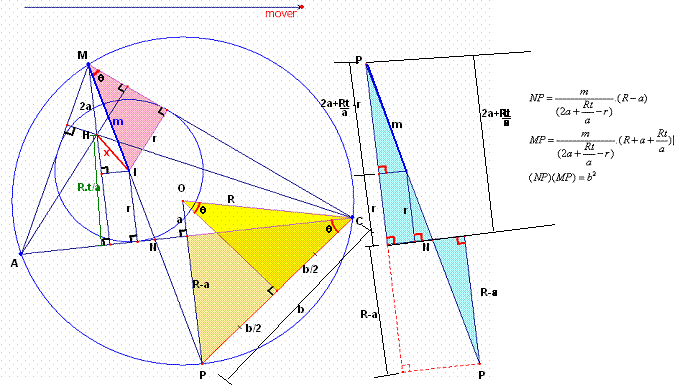
Triángulos sombreados semejantes ![]()
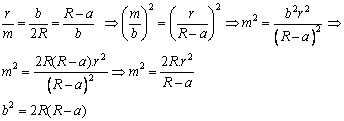
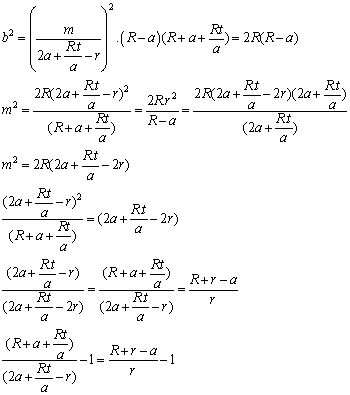

Sumando (I) y (II) obtenemos:
![]()