Propuesto
por Juan Carlos Salazar, Profesor de Geometría del Equipo Olímpico de Venezuela.(Puerto Ordaz).
De
Investigación
Problema 389.
En el triángulo ABC se tiene <B=30º, <C=20º, D en BC con
BD=AC. Hallar <DAC.
Salazar,
J. C. (2004): Comunicación personal.
Solución.-
Construimos el triángulo isósceles CBA’ tomando como ángulo desigual el de 20º y lados iguales a a=CB. Un cómputo elemental de los ángulos nos conduce a que el triángulo AA’B es isósceles y con lados iguales (A’A=A’B) a a-b. El lado desigual es c=AB, que puede expresarse en función de a-b. Se tiene c=2·(a-b)·cos 50º.
Aplicando el teorema de los senos al triángulo ABC se tiene
a =sen A·![]() =sen 130º ·
=sen 130º ·![]() =
=![]() =
=![]() .
.
El valor del tercer lado también
puede expresarse en función de a-b.
b=a - (a-b)
= ![]() - (a-b) = (a-b)·
- (a-b) = (a-b)·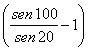 = (a-b)
= (a-b) ![]() =
=
=(a-b) ·![]() después de aplicar las fórmulas de diferencias de senos.
después de aplicar las fórmulas de diferencias de senos.
Si tomamos para a-b un valor numérico concreto tendremos un triángulo semejante al del problema. Por sencillez en los cálculos vamos a tomar a-b =sen 20. Con este dato, los lados del triángulo son:
a = sen 100= sen 80; b= sen
40= cos 50 y finalmente c=2
·sen 20· cos
50º, como se muestra en la figura.
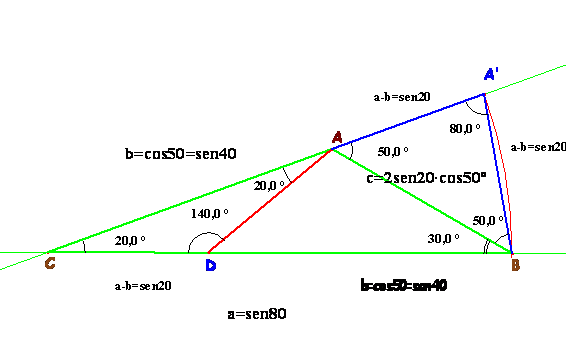
Calculamos d=AD aplicando el teorema del coseno al triángulo ACD. Tenemos en él
d2 = sen2 40º + sen2 20º - 2· sen 40º· sen 20º cos 20º = sen2 40º + sen2 20º - sen2 40º
Por tanto d= sen 20º, lo que significa que este triángulo es isósceles siendo iguales los lados DC y DA, y de ello el ángulo DAC mide 20º.