Propuesto por Juan Carlos Salazar, Profesor de Geometría del Equipo Olímpico de Venezuela.(Puerto Ordaz).

De Investigación

Problema 389.

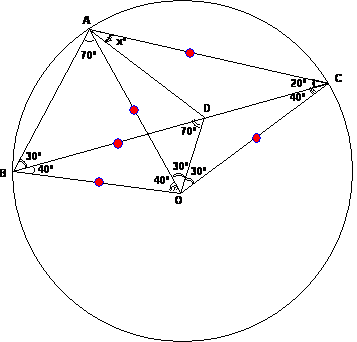
En el triángulo ABC se tiene <B=30º, <C=20º, D en BC con BD=AC.

Hallar <DAC.

Salazar, J. C. (2004): Comunicación personal.

Resolución de William Rodríguez Chamache

Trazamos la circunferencia circunscrita del triángulo ABC de centro O

Luego el triángulo AOC es equilátero AC=OC=OA

Triángulo BOC es isósceles (OB=OC) también triángulo AOB isósceles (OA=OB)

Pero observamos que los segmento AD=DC por lo tanto x=20