Problema 390

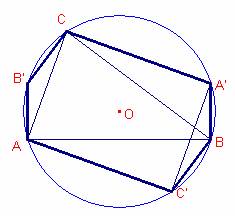
Siga un triangle acutangle i la seua circumferència circumscrita. Cada radi que parteix de cadascun dels vèrtex es prolonga fins la circumferència. S’uneixen dos a dos les extremitats dels diàmetres així construïts. Demostreu que l’àrea de l’hexàgon obtingut és doble de l’àrea del triangle.

Solució de Ricard Peiró:

Considerem el triangle acutangle.

Siga R el radi de la circumferència circumscrita al triangle . L’àrea del triangle és .

.

Siga el simètric del triangle respecte del centre O de la circumferència circumscrita del triangle .

Els triangles , són simètrics respecte del punt O.

AC’A’C és un quadrilàter inscriptible i , aleshores és un rectangle.

Aplicant el teorema de Pitàgores:

.

Anàlogament, , .

El quadrilàter ABCB’ és inscriptible aleshores .

L’àrea de l’hexàgon AC’BA’CB’ és igual a l’àrea del rectangle AC’A’C més dues vegades l’àrea del triangle .

Calculem l’àrea de l’hexàgon AC’BA’CB’:

Aplicant el teorema dels sinus: :

.
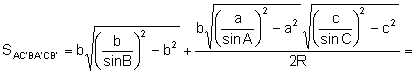
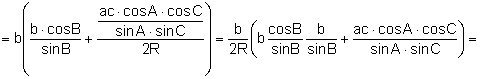