Problema 390

Se tiene un triángulo y su circunferencia circunscrita: cada radio que parte de cada uno de los vértices se prolonga hasta la circunferencia. Se unen dos a dos las extremidades de los tres diámetros así construidos; demostrar que la área del hexágono obtenido es doble de la del triángulo (N.A. 1844, p. 317)

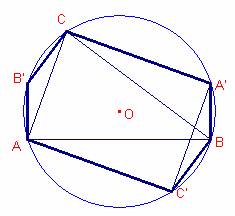Solución de Ricard Peiró:

Consideremos el triángulo acutángulo.

Sea R el radio de la circunferencia circunscrita al triángulo . El área del triángulo es .

.

Sea el simétrico del triángulo respecto del centro O de la circunferencia circunscrita del triángulo .

Los triángulos , son simétricos respecto del punto O.

AC’A’C es un cuadrilátero inscriptible y , entonces es un rectángulo.

Aplicando el teorema de Pitágoras:

.

Análogamente, , .

El cuadrilátero ABCB’ es inscriptible entonces .

El área del hexágono AC’BA’CB’ es igual al área del rectángulo AC’A’C más dos veces el área del triángulo .

Calculemos el área del hexágono AC’BA’CB’:

Aplicando el teorema de los senos: :

.
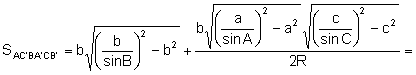