Problema
390.
Teorema 522.
1553. Se tiene un triángulo y su circunferencia
circunscrita: cada radio que parte de cada uno de los vértices se prolonga
hasta la circunferencia. Se unen dos a dos las extremidades de los tres
diámetros así construidos; demostrar que el área del hexágono obtenido es doble
de la del triángulo (N.A. 1844, p. 317).
Frère Gabriel Marie (FGM), 1820-1891. 5. ed.:3 p.
L., [iii]-xxiv, 1302 p. diagrs.
Solución de Saturnino Campo Ruiz,
profesor del IES Fray Luis de León, de Salamanca.-
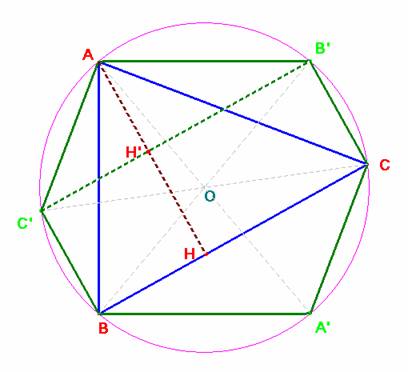
Al ser diámetros los
segmentos MM’, se tiene que los
ángulos B’CB, CBC’, BC’B’ y
C’B’C son rectos, por tanto, el cuadrilátero BC’B’CB es un
rectángulo.
La altura desde A del triángulo ABC, es igual a la altura h’=
AH’ del triángulo AC’B’ más la altura B’C del rectángulo BC’B’CB. Por simetría
respecto de O los triángulos AC’B’ y A’CB son congruentes.
Por tanto, si denotamos
por [MNP] el área del polígono MNP
se tiene:
2[ABC]= 2[AB’C’] + [BC’B’C] = [AB’C’] + [BC’B’C]
+[A’BC] = [BC’AB’CA’], que es
lo que pretendíamos demostrar.