Problema 392.- Si en un triángulo se verifica que cos A + cos B = 4 sen ² (C/2), entonces, a+b=2c.

Zegarra, L. http://www.luiszegarra.cl/main.htm (guía 2_4-pdf, cap 5).

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca.-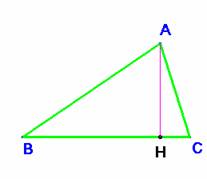

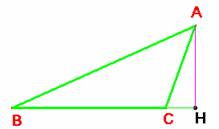En cualquier triángulo un lado, por ejemplo a=BC, es la suma de las proyecciones de los otros dos sobre él, en el acutángulo, a = BC = BH + CH y en el obtusángulo, a = BC = BH – CH. El signo – o + lo da el coseno del ángulo C en este caso. Podemos pues poner, en general, a=BC= BH ± CH= c cos B + b cos C. Si hacemos lo mismo con el lado b=AC tendremos

a = c cos B + b cos C

b = c cos A + a cos C

Sumándolas:

(a+b) = (a+b) cos C + c (cos A + cos B) o bien

(a+b)(1– cos C) = c(cos A +cos B).

Ahora aplicamos que 1– cos C=2 sen ²(C/2), según las fórmulas del ángulo mitad

2(a+b) sen ²(C/2)= c(cos A + cos B) (1)

y, por la hipótesis del enunciado, cos A +cos B =4 sen ²(C/2) (0)

2(a+b) sen ²(C/2)= 4 c sen ²(C/2), y simplificando

a+b=2c (2)

como se pretendía demostrar.

Recíprocamente si partimos de la relación (2) entre los lados, como en todo triángulo se verifica (1) tendríamos 4c sen ²(C/2) = c(cos A + cos B) que implica (0), luego la condición es necesaria y suficiente.