Problema 395.

Siguen A, B, C, D punts colineals en aquest ordre. Dibuixem els triangles equilàters  i  en el mateix semiplànol.

Siga G la intersecció de les circumferències circumscrites a  i , que està en el mateix semiplànol que E i F. Demostreu que .

Solució Ricard Peiró:

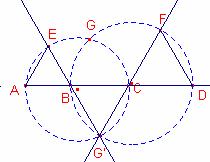Considerem les rectes EB i FC que s’intersecten en el punt G’.

Notem que el triangle  és equilàter.

Vegem que el quadrilàter AECG’ és inscriptible.

Els triangles ,  són iguals. Siga .

Aleshores, .

Per tant, , , és a dir, són suplementaris.

Per tant, aplicant el teorema de Tolomeu,  AECG’ és inscriptible.

Anàlogament BG’DF és un quadrilàter inscriptible.

Considerem les circumferències circumscrites als triangles a  i .

G’ pertany a ambdues circumferències.

Siga G la intersecció de les circumferències circumscrites a  i , que està en el mateix semiplànol que E i F.

Per ser angles inscrits i abraçar el mateix arc:

.

.

Aleshores, .

Amb Cabri:

Figura barroso395.fig

Applet created on 2/06/07 by Ricard Peiró with CabriJava