Problema 395.

Siguen A, B, C, D puntos colineales en este orden. Dibujemos los triángulos equiláteros  y  en el mismo semiplano.

Sea G la intersección de las circunferencias circunscritas a  y , que está en el mismo semiplano que E y F. Demostrar que .

Solución Ricard Peiró:

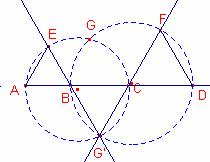Consideremos las rectas EB i FC que se intersectan en el punto G’.

Notemos que el triángulo  es equilátero.

Veamos que el cuadrilátero AECG’ es inscriptible.

Los triángulos ,  son iguales. Sea .

Entonces, .

Por tanto, , , es decir, son suplementarios.

Por tanto, aplicando el teorema de Tolomeo,  AECG’ és inscriptible.

Análogamente BG’DF es un cuadrilátero inscriptible.

Consideremos las circunferencias circunscritas a los triángulos a  y .

G’ pertenece a ambas circunferencias.

Sea G la intersección de las circunferencias circunscritas a  y , que está en el mismo semiplano que E i F.

Por ser ángulos inscritos y abarcar el mismo arco:

.

.

Entonces, .

Con Cabri:

Figura barroso395.fig

Applet created on 2/06/07 by Ricard Peiró with CabriJava