Problema 397

PRUEBAS PRIMER DÍA

Guayaquil, 26 de septiembre de 2006

PROBLEMA 1

En un triangle rectangle escalè ,  es consideren les circumferències inscrita i circumscrita. La recta tangent en A la circumferència circumscrita talla la recta BC en M. Siguen S i R els punts de tangència de la circumferència inscrita amb els catets  i , respectivament. La recta RS talla la recta BC en N. Les rectes AM i RS es tallen en U. Demostreu que el triangle  és isòsceles.

21ª OIM (2006). Guayaquil (Ecuador)

Solució de Ricard Peiró (IES "Abastos" València).:

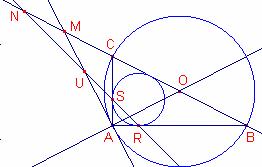
Com que el triangle rectangle ,  és escalè, siga .

Siga O el centre de la circumferència circumscrita.

La mitjana del triangle rectangle referida a la hipotenusa mesura igual que el radi de la circumferència circumscrita, i el centre de la circumferència circumscrita és el punt mig de la hipotenusa.

Aleshores, el triangle  és isòsceles, .

La recta AM és tangent a la circumferència circumscrita aleshores:

 són perpendiculars, per tant, .

Per ser , , i R i S els punts de tangència.

 és rectangle i isòsceles. Aleshores, .

Per tant, .

, Aleshores, .

Aleshores, . Aleshores, el triangle  és isòsceles, .

Nota si el triangle ,  és isòsceles les rectes RS i BC són paral·leles i no es pot formar el triangle .

Amb Cabri:

Figura barroso397.fig

Applet created on 16/06/07 by Ricard Peiró with CabriJava