Problema 397
PRUEBAS PRIMER DÍA
Guayaquil, 26 de septiembre de 2006
PROBLEMA 1
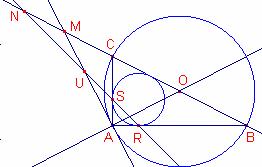
En el triángulo escaleno ABC, con <BAC=90o, se consideran las circunferencias inscrita y circunscrita. La recta tangente en A a la circunferencia circunscrita corta a la recta BC en M. Sean S y R los puntos de tangencia de la circunferencia inscrita con los catetos AC y AB, respectivamente. La recta RS corta a la recta BC en N. Las rectas AM y SR se cortan en U. Demuestre que el triángulo UMN es isósceles.
21ª OIM (2006). Guayaquil (Ecuador)
Solución de Ricard Peiró (IES "Abastos" València.):
Como que el triángulo rectángulo 
, 
es escaleno, siga 
.
Siga O el centre de la circunferencia circunscrita.
La mediana del triángulo rectángulo referida a la hipotenusa mide igual que el radio de la circunferencia circunscrita, y el centro de la circunferencia circunscrita es el punto medio de la hipotenusa.
Entonces, el triángulo 
es isósceles, 
.
La recta AM es tangente a la circunferencia circunscrita entonces:
son perpendiculares, por tanto, 
.
Por ser , , y R, S los puntos de tangencia.
es rectángulo y isósceles. Entonces, 
.
Por tanto, 
.
, Entonces, 
.
Entonces, 
. Entonces, el triángulo 
es isósceles, 
.
Nota si el triángulo , es isósceles las rectas RS y BC son paralelas y no se puede construir el triángulo .
Con Cabri:
Figura barroso397.fig
Applet created on 16/06/07 by Ricard Peiró with CabriJava