PRUEBAS PRIMER DÍA

Guayaquil, 26 de septiembre de 2006

PROBLEMA 1

En el triángulo escaleno ABC, con <BAC=90^o, se consideran las circunferencias inscrita y circunscrita. La recta tangente en A a la circunferencia circunscrita corta a la recta BC en M. Sean S y R los puntos de tangencia de la circunferencia inscrita con los catetos AC y AB, respectivamente. La recta RS corta a la recta BC en N. Las rectas AM y SR se cortan en U. Demuestre que el triángulo UMN es isósceles.

21ª OIM (2006). Guayaquil (Ecuador)

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca

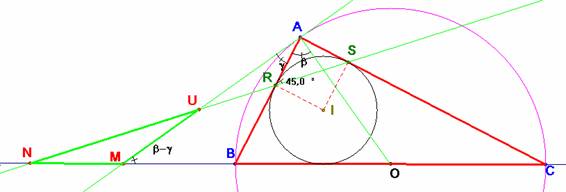
Se trata de un simple recuento de ángulos.

Llamemos a =90, b y g a los ángulos del triángulo ABC.

1.-  El triángulo ARS es rectángulo isósceles, por tanto <ARS=45º.

2.-  El triángulo BAO es isósceles, luego <OAB= b=OBA.

3.-  El triángulo MAO es rectángulo en A de lo cual se deduce que <MAB = g.

4.-  <NUM=<AUR = <ARS- <MAB =45º- g.

5.-  En el triángulo MAB se tiene que <AMB = <OBA- <MAB= b- g.

6.-  Por último en el triángulo UNM se tiene:

< UNM=<AMB- <NUM = (b- g)-(45º- g) = b-45º= 45º- g = <NUM.                     c.q.d.