Problema 398

Sean ABC un triángulo no rectángulo en A y V un punto situado sobre la recta BC, distinto de los vértices. La paralelas a AC y AB por por V cortan a AB y AC en D y E, respectivamente. La perpendicular a AB por V corta en en G a AC. La perpendicular a AC por V corta en F a AB. Además consideramos los puntos de intersección J = GD Ç VF y K =EF Ç VG.

a) Demostrar que cada uno de los siguientes enunciados es cierto si y solo si AV es una de las bisectrices del ángulo A.

1. DE es paralela a FG.
2. FG es paralela a JK.
3. DG, EF y AV son concurrentes.
4. El triángulo VFG es isósceles.

b) V es el ortocentro de AFG.

Romero, J.B. y García, F.J. (2007): Comunicación personal.

Solución parcial del director.

Tracemos el triángulo y las rectas dadas.

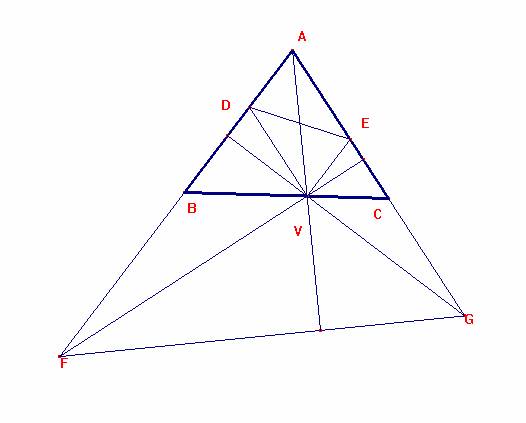
Caso a) 1.- Veamos que sólo si AV es la bisectriz interior, DE es paralela a FG.

Sean <VAC=α y <VAB=β.

Es por construcción, <AGF=90-α, por ser AV perpendicular a FG.

Supongamos ahora que DE es paralela a FG.

Debe ser <AED=<AGF=90-α.

Por tanto las diagonales del paralelogramo ADVE tendrán que ser perpendiculares, por lo que ADVE tendrá que ser rombo, y tendría que ser <VAE=VAD=α, y AV ser la bisectriz interior.

 

Veamos ahora que si AV es bisectriz interior, DE es paralela a FG

Si AV es bisectriz, con <VAE=VAD=α  el triángulo AFG tiene una altura que es bisectriz, por lo que es isósceles y <AGF=<AFG=90-α.

En tal caso, el cuadrilátero ADVE es rombo y sus diagonales son perpendiculares. Se tiene pues que <AED=90-α, y  de ahí lo pedido.

.   

a) Demostrar que cada uno de los siguientes enunciados es cierto si y solo si AV es una de las bisectrices del ángulo A.

2. FG es paralela a JK.

Sólo veré la implicación directa:

Supongamos que AV es la bisectriz interior.

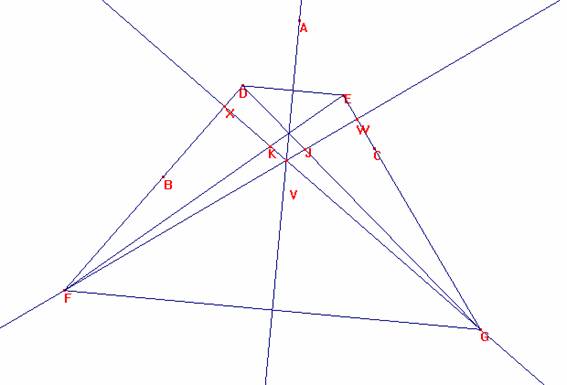
Consideremos el trapecio isósceles DEGF.

Las diagonales DG y EF son iguales

Los ángulos <DGE y <EFD son iguales.

Los triángulos rectángulos FWG y GXF son simétricos respecto a AV.

Por ello,  los triángulos WJG y XKF también lo son. Así K es el simétrico de J según AV, y JK es paralelo a FG.

a) Demostrar que cada uno de los siguientes enunciados es cierto si y solo si AV es una de las bisectrices del ángulo A.

3. DG, EF y AV son concurrentes.

Sólo veré la implicación directa:

Supongamos que AV es la bisectriz interior.

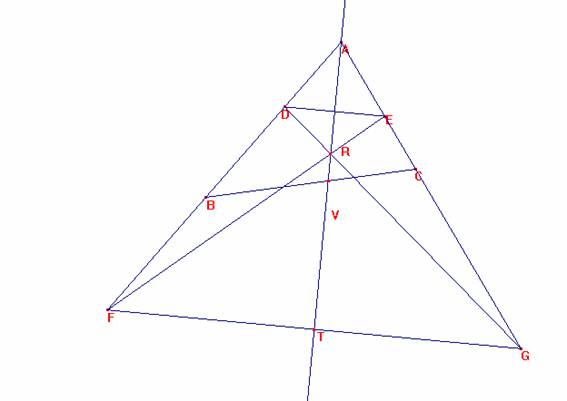
Los triángulos ADE y AFG son isósceles y semejantes, de los que AV es bisectriz y altura.

Luego es AD=AE, DF=EG, FT=FG. Así, por el teorema de Ceva, DG, EF y AV concurren en R

a) Demostrar que cada uno de los siguientes enunciados es cierto si y solo si AV es una de las bisectrices del ángulo A.

 

4.- El triángulo VFG es isósceles.

Comencemos demostrando que sólo si es AV la bisectriz interior, VFG es isósceles.

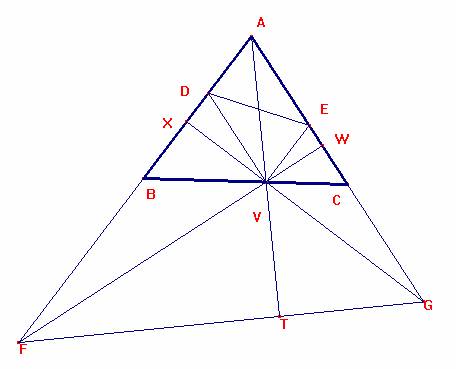
Supongamos que AV no sea bisectriz de ABC, y sean <BAV=α, y <CAV=β.

Por ser GV y FV alturas de AFG, es <AGT=90-β, por lo que <GFV=<GFW=β,

y de igual manera, <FGV=<FGX=α.

Si α ≠ β, es decir, si AV no es bisectriz, el triángulo VFG no es isósceles.

Si α=β, es decir, si AV es la bisectriz interior, el triángulo VFG sí es isósceles.  

Caso  b).

En todos los casos de construcción de AV, al ser GV y FV alturas de AFG, por construcción, luego AV es también altura y  V es su ortocentro.

Ricardo Barroso Campos

Didáctica de las Matemáticas.

Universidad de Sevilla.