Problema 398 de triánguloscabri

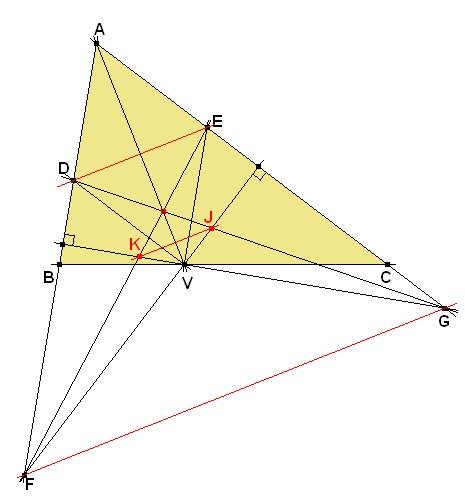
Sean ABC un triángulo no rectángulo en A y V un punto situado sobre la recta BC, distinto de los vértices. La paralelas a AC y AB por por V cortan a AB y AC en D y E, respectivamente. La perpendicular a AB por V corta en en G a AC. La perpendicular a AC por V corta en F a AB. Además consideramos los puntos de intersección J = GD Ç VF y K =EF Ç VG.

a) Demostrar que cada uno de los siguientes enunciados es cierto si y solo si AV es una de las bisectrices del ángulo A.

DE es paralela a FG.
FG es paralela a JK.
DG, EF y AV son concurrentes.
El triángulo VFG es isósceles.

b) V es el ortocentro de AFG.

Propuesto por Juan Bosco Romero Márquez y Francisco Javier García Capitán

Solución de Francisco Javier García Capitán

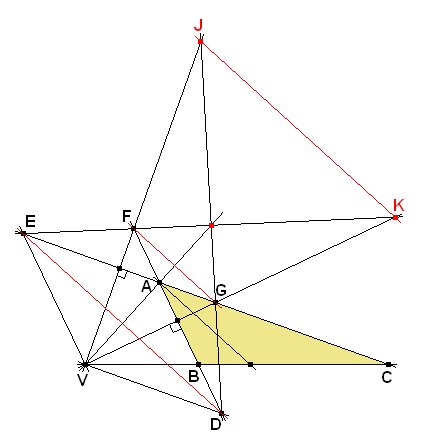
Usaremos coordendas baricéntricas y Mathematica para resolver a la vez cada enunciado y su recíproco.

Introducimos los puntos del problema.

Obtenemos, en forma factorizada, las expresiones que deberán anularse para que se cumplan cada uno de los enunciados 1., 2. y 3., teniendo en cuenta que

dos rectas serán paralelas cuando se cortan en un punto cuyas coordenadas suman cero, es decir, un punto del infinito, y que
tres rectas son concurrentes cuando se anula el determinante de sus coeficientes.

La cuestión sobre el triángulo isósceles VFG la resolvemos usando la función CuadradoDistancia.

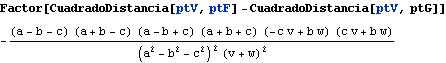
Ahora, I=(a:b:c) es el incentro, y las rectas cy + bz = 0, cy - bz = 0 son las ecuaciones de las bisectrices interior y exterior del ángulo A, lo que resuelve el apartado a).

Para el apartado b) hacemos

lo que indica que V es siempre el ortocentro de AFG.