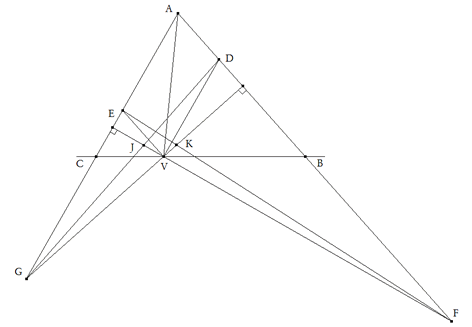
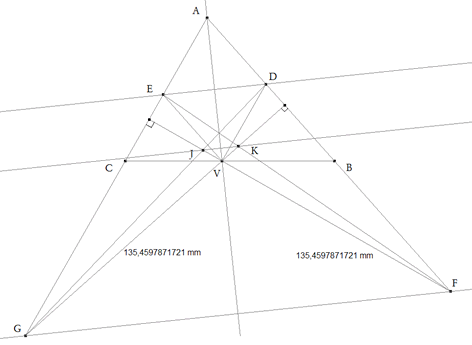
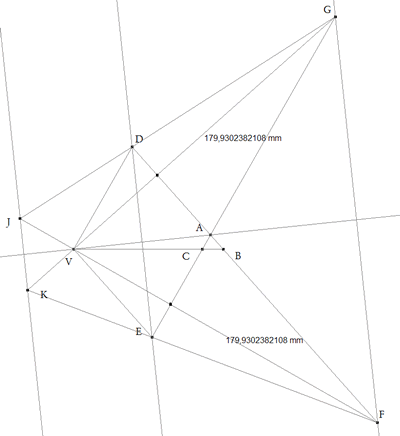
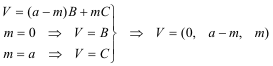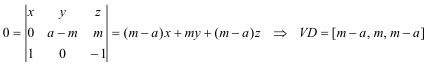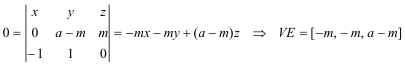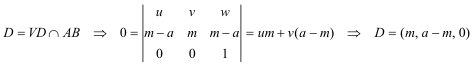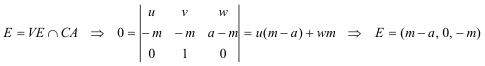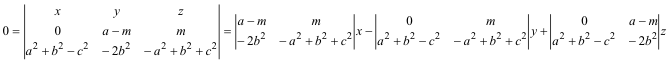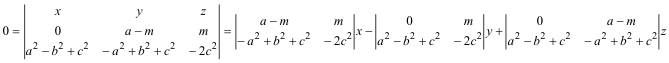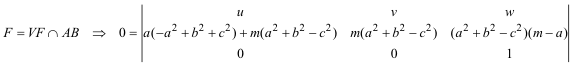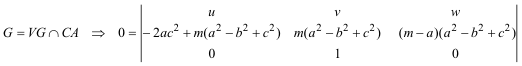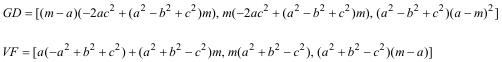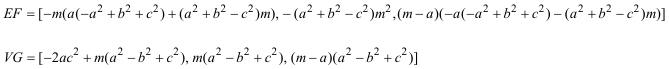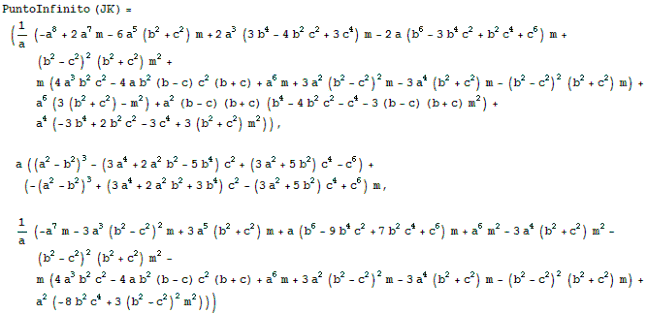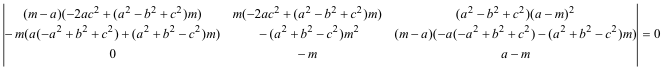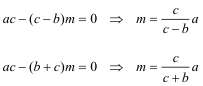De investigación. Propuesto por Juan Romero Márquez y Francisco Javier García Capitán. Problema 398. Sean ABC un triángulo no rectángulo en A y V un punto situado sobre la recta BC, distinto de los vértices. La paralelas a AC y AB por V cortan a AB y AC en D y E, respectivamente. La perpendicular a AB por V corta en G a AC. La perpendicular a AC por V corta en F a AB. Además consideramos los puntos de intersección J = GD VF y K =EF VG. a) Demostrar que cada uno de los siguientes enunciados es cierto si y solo si AV es una de las bisectrices del ángulo A.
1. DE es paralela a FG. 2. FG es paralela a JK. 3. DG, EF y AV son concurrentes. 4. El triángulo VFG es isósceles. b) V es el ortocentro de AFG. Romero, J. y García, F.G. (2007): Comunicación personal. Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (3 de julio de 2007) |
|
OBTENCIÓN DE LOS DATOS DEL ENUNCIADO |
|
Para hallar la solución, usaremos coordenadas baricéntricas. Es conveniente echar mano de Francisco Javier García Capitán: http://garciacapitan.auna.com/baricentricas/ Paul Yiu: www.math.fau.edu/yiu/GeometryNotes020402.ps Las coordenadas baricéntricas de los vértices del triángulo ABC son:
Las coordenadas baricéntricas de los lados del triángulo ABC son:
Usamos como siempre
Mediante el parámetro m, definimos V como un punto cualquiera sobre el lado BC
Dibujamos ahora el enunciado.
RECTA VD La recta VD debe ser paralela a la recta CA, tienen en común el mismo punto de infinito. En coordenadas baricéntricas el punto de infinito de una recta es:
Por lo tanto el punto de infinito de la recta CA es
Podemos definir la recta VD como la recta que pasa por el punto V y el PuntoInfinito(CA)
RECTA VE Análogamente al párrafo anterior, obtenemos VE como la recta por el punto V y el PuntoInfinito(AB)
PUNTO D Obtenemos el punto D como la intersección de las dos rectas VD y AB
PUNTO E
RECTA VF La recta VF es perpendicular a la recta CA. Sea una recta dada con punto de infinito en
entonces el punto de infinito de cualquier recta perpendicular a la recta dada es el punto de infinito de la recta
donde
En nuestro caso la recta dada es CA y su punto de infinito es
por lo que buscaremos el punto de infinito de
que es, eliminando el factor ½,
y por lo tanto la perpendicular por V a la recta CA es la recta por V y este último punto
de donde
RECTA VG Es la recta por V perpendicular a AB.
y por lo tanto la recta buscada nos la da
de donde
PUNTO F Obtenemos el punto F como intersección entre la recta VF y la recta AB
de donde
PUNTO G
de donde
PUNTO J Obtenemos el punto J como la intersección de las rectas GD y VF
de donde
PUNTO K
de donde
|
|
APARTADO a |
|
APARTADO a.1 - DE es paralela a FG. Si DE es paralela a FG es que coinciden en el punto de infinito y por lo tanto
de donde
Expresando que las componentes son proporcionales tenemos
que nos conduce a las dos ecuaciones que son idénticas a la ecuación a.1
APARTADO a.2 - FG es paralela a JK. Si JK es paralela FG
Expresando que las componentes son proporcionales tenemos
que nos conduce a las dos ecuaciones que son idénticas a la ecuación a.2
APARTADO a.3 - DG, EF y AV son concurrentes. Si las tres rectas son concurrentes su determinante se anula
que nos conduce a la ecuación a.3
APARTADO a.4 - El triángulo VFG es isósceles. Si el triángulo es isósceles entonces
Para ello usaremos la fórmula de la distancia al cuadrado D2 entre dos puntos dados por sus coordenadas baricéntricas.
Y en nuestro caso
que nos conduce a la siguiente ecuación a.4
CONCLUSIÓN - Aparatado a. La condición de que V sea el pie de la bisectriz del ángulo A es
que nos conduce a
El factor común de las cuatro ecuaciones ecuación a.1, ecuación a.2, ecuación a.3, ecuación a.4 es
que como acabamos de ver expresa la condición de que V sea el pie de la bisectriz del ángulo A.
Los dos posibles valores de m son respectivamente para la bisectriz externa y para la bisectriz interna. Podemos pues enunciar LA CONDICIÓN NECESARIA Y SUFICIENTE PARA QUE SE CUMPLAN LOS CUATRO RESULTADOS DEL APARTADO a ES QUE V SEA EL PIE DE UNA DE LAS DOS BISECTRICES DEL ÁNGULO A.
BISECTRIZ INTERNA
BISECTRIZ EXTERNA
|
|
APARTADO b |
|
Basta leer el enunciado para comprobar que V se encuentra sobre la perpendicular desde F al lado AG=CA. Basta leer el enunciado para comprobar que V se encuentra sobre la perpendicular desde G al lado AF=AB. V es pues por definición, en el enunciado, el ortocentro del triángulo AFG. |