De investigación.

Propuesto por Juan Bosco Romero Márquez y Francisco Javier García Capitán.

Problema 398.-  Sean ABC un triángulo no rectángulo en A y V un punto situado sobre la recta BC, distinto de de los vértices. Las paralelas a AC y AB por V cortan a AB y AC en D y E respectivamente. La perpendicular a AB por V corta en G a AC. La perpendicular a AC por V corta en F a AB. Además consideramos los puntos de intersección J = GD∩VF y K = EF∩VG.

a) Demostrar que cada uno de los siguientes enunciados es cierto si y sólo si AV es una de las bisectrices del ángulo A.

       1. DE es paralela a FG.

       2. FG es paralela a JK.

       3. DG, EF y AV son concurrentes.

       4. El triángulo VFG es isósceles.

b) V es el ortocentro de AFG.

Romero, J. y García, F.G. (2007). Comunicación personal.

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca .-

Nos apoyamos básicamente en dos propiedades.

Propiedad 1. (Problema nº 68 de esta colección).

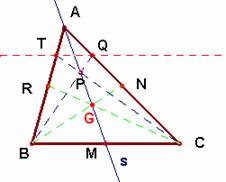
Dado un triángulo ABC, tracemos la recta s que contiene a la mediana AM. Tomemos P, un punto cualquiera de s. Tracemos las rectas BP y CP, que cortarán a AC y a AB, o sus prolongaciones, en Q y T. Entonces TQ es paralela a BC. Y recíprocamente.

Propiedad 2. (Alineación de los puntos medios de los vértices opuestos de un cuadrilátero completo).

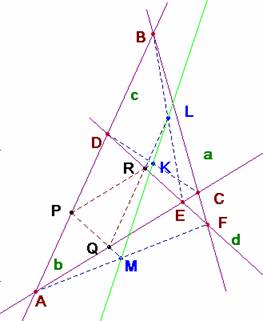
Un cuadrilátero completo consta de cuatro rectas a, b, c, y d de las que tres cualesquiera de ellas no son concurrentes y sus seis puntos de intersección.

Las cuatro rectas son llamadas lados y los seis puntos vértices. Dos vértices que no están sobre un mismo lado se llaman opuestos.

En un cuadrilátero completo a, b, c, d, están alineados los puntos medios de sus segmentos diagonales (=formados con dos vértices opuestos).

En la figura son líneas diagonales las rectas AF; EB y CD. Los puntos medios de estos segmentos son K, L y M.

La demostración se basa en tomar un triángulo formado por tres lados y el cuarto como transversal y aplicar el teorema de Menelao.

Resolución del problema

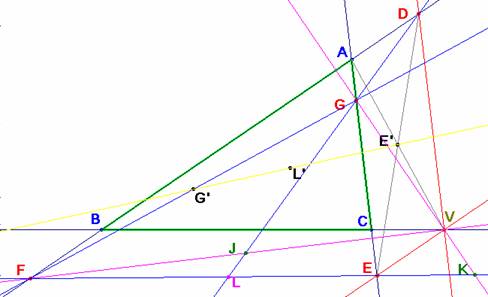
b) Que V es el ortocentro de AFG se deduce de inmediato de la construcción. También que A es el ortocentro de VFG.

a) Voy a llamar proposición 0 a AV es una de las bisectrices del ángulo A. Trataremos de demostrar la equivalencia de las otras cuatro proposiciones con ésta.

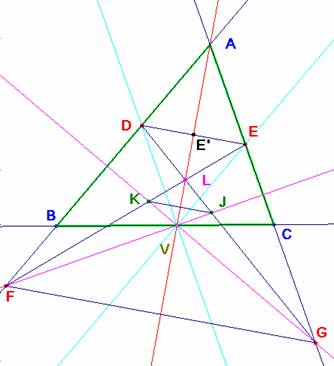
Situación cuando AV es la bisectriz interior del ángulo A.

0 1

El cuadrilátero ADVE es un paralelogramo. Su centro es E’. Si AV es bisectriz de ABC, el paralelogramo es un rombo, y AV una diagonal, por tanto perpendicular a DE. Al ser también altura de AFG, se concluye que DE y FG son paralelos.

1 3  

Si DE||FG , la recta AE’ = AV  es mediana de los triángulos ADE y AFG. Tomando L= FE∩GD resulta que L está sobre la mediana AV de AFG y de ADE (propiedad 1).

3 2

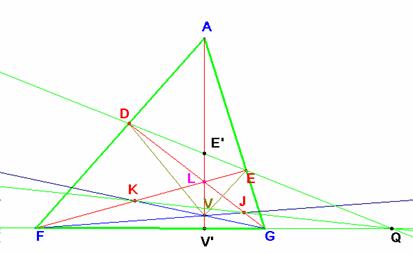
Sea Q = DE∩FG.

 Por  ser E’ el punto medio de DE se tiene: (QV’GF)= –1= (QE’ED), Q está en el infinito y V’=G’  es el punto medio de FG. En resumen, AV es la mediana de AFG, y también de LFG, por tanto, las proyecciones de la base por V forman el segmento JK paralelo a ésta.  Y también concurre en Q.

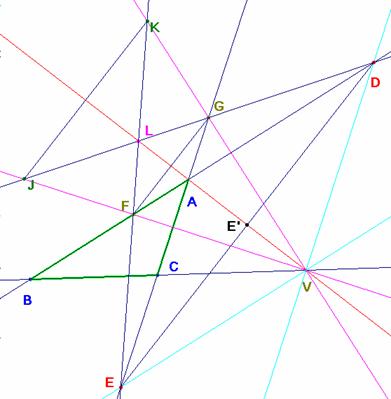
Situación cuando AV es la bisectriz exterior.

2 4

Si JK||FG  de nuevo tomando L= FE∩GD resulta que LV es mediana del triángulo LFG (propiedad 1). Queremos concluir que L está alineado también con A (y por tanto con E’) y entonces AV=LV será, además de altura sobre FG, bisectriz y mediatriz de AFG y de VFG. Y por tanto estos triángulos serán isósceles.

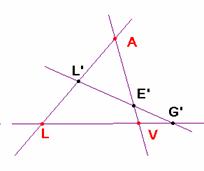Considero el cuadrilátero completo formado a partir del triángulo AGD y la transversal EF.  Son sus vértices A, G, D, E, F y L. Son opuestos F y G, D y E y  A y L. Sus puntos medios respectivos G’, E’ y L’ han de estar alineados (Propiedad 2).

Si los puntos A, L y V no están alineados, tenemos:

L’= punto medio de AL. E’= punto medio de DE (y de AV) y G’= punto medio de FG, que está sobre LV ya que ésta es mediana del triángulo LFG.

De esa situación se deduce que L’E’ y LV son paralelos y con ello G’, el punto medio de FG, está en el infinito, lo cual es absurdo, salvo si <BAC=90º. En consecuencia A, L y V están alineados y se concluye la demostración.

4 0

Si VFG es isósceles, la altura por V (AV) es también la bisectriz del ángulo FVG y mediatriz de FG, por tanto también es isósceles AFG, y AV es mediana, mediatriz, altura y por tanto, también bisectriz de AFG y de ABC.