Problema 399

Construcción del triángulo equilátero dada la altura (ha).

Rendón, A. (2000) Geometría paso a paso. Volumen 1. Elementos de geometría métrica y sus aplicaciones en arte, ingeniería y construcción. Editorial Tébar. (p. 78)

Estrategias de soluciones del director.

 Primera, Euclidea

Por un extremo del segmento  ha se construye la recta perpendicular a.

Por el otro extremo del mismo se gira 30º la recta que contiene ha.

Se toma la simétrica de la recta girada.

Las intersecciones de ambas rectas con a, son B y C.

ABC es equilátero y ha es su altura.

Segunda, mediante la construcción del lado del equilátero

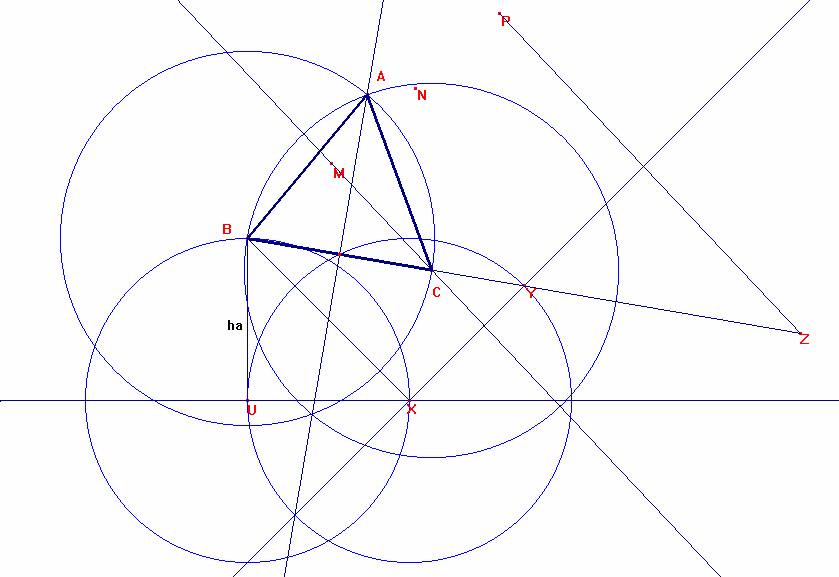
Sea ha la altura dada.

Si a es el lado del triángulo a/2, ha, a son lados de un triángulo rectángulo, ha² + (a/2)² =a²

Luego es : .

Si BU=ha, y UX =ha es perpendicular a BU, .

Tomemos XY=ha y perpendicular a BX, es

Sea Z el simétrico de B respecto a Y. Es .

Tomemos un punto M. Sea N el simétrico de B respecto a M y P el simétrico de M respecto a N.

Así, si construimos la recta PZ y la paralela por M a PZ, que cortará a la recta BY en C, tendremos que .

Con dos circunferencias de radio a y centro B y C, tenemos A.

ABC cumple lo establecido.

Ricardo Barroso Campos

Didáctica de las matemáticas.

Universidad de Sevilla