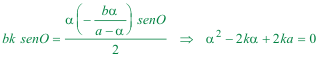APOLONIO, HALLEY,NEWTON, PETERSEN, SAPIÑA, RITT, ROSILLO - LA SEMEJANZA

*La intención de este documento es descubrir la SEMEJANZA como herramienta para estudiar las figuras geométricas. Se establecen los resultados fundamentales más simples.** José María Pedret. Ingeniero Naval. Esplugues de Llobregat (Barcelona).2007
Apolonio	Halley	Newton	Petersen
	Sapiña	Ritt**
( ) Una vez establecidos los RESULTADOS anteriores, usaremos la semejanza para resolver los problemas que se proponen. Aunque presentaremos también otros métodos de resolución. (*) Además de la de Georges Ritt, se incluye la solución al segundo problema del profesor Nicolás Rosillo, Dpto. Matemáticas, IES Máximo Laguna (Santa Cruz de Mudela, Ciudad Real). VERSION 4


ENUNCIADOS

PRIMER PROBLEMA

Este es el problema tipo a resolver, con regla y compás, usando un mínimo de teoría de la semejanza. Es el modelo más simple del problema siguiente: "...Colocar un triángulo, semejante a un triángulo dado, de tal manera que uno de sus vértices esté en un punto dado y que los otros dos se hallen sobre dos curvas dadas..." Julius Petersen. Méthodes et théories pour la résolution des problèmes de constructions géométriques. Gauthier-Villars. Paris (1880); PROBLÈME 349. Juan Sapiña Borja. Problemas gráficos de Geometría. Litograf. Madrid 1955. Capítulo de triángulos, PROBLEMA 346. Enunciado Colocar un triángulo equilátero, de tal manera que sus vértices estén sobre tres rectas paralelas dadas. Un de los vértices puede colocarse en cualquiera de las rectas; éste será el centro de rotación; el ángulo de giro será de 60º y la razón de homotecia 1.

SEGUNDO PROBLEMA

Este problema fue propuesto y resuelto por APOLONIO en su obra "De Sectione Spatii". La obra se perdió, pero HALLEY la restableció a partir de una traducción árabe. Julius Petersen. Méthodes et théories pour la résolution des problèmes de constructions géométriques. Gauthier-Villars. Paris (1880); PROBLÈME 366. Juan Sapiña Borja. Problemas gráficos de Geometría. Litograf. Madrid 1955. Capítulo de áreas, PROBLEMA 637. Georges Ritt. Problèmes d’application de algèbre à la géométrie avec les solutions développées. Librairie de L. Hachette. Paris. 1857.PROBLEME LXX. Nicolás Rosillo, profesor del Dpto. Matemáticas, IES Máximo Laguna (Santa Cruz de Mudela, Ciudad Real). TRIANGULOSCABRI. Problema 256. Enunciado Por un punto dado P, trazar una recta que forme con otras dos rectas dadas, un triángulo de área dada. Sea A el punto de intersección de las rectas dadas; se representa el área dada bajo la forma de un triángulo, del que un lado es AP y el otro está sobre una de las rectas dadas. La recta buscada debe ser tal que el elemento de área que se añade al triángulo sea igual al que determina la sección en el triángulo. Pero esas dos áreas son triángulos cuyas alturas son conocidas. La razón de las bases de esos triángulos es pues conocida también y en consecuencia, el problema se transforma en el enunciado auxiliar que sigue. Enunciado, también de APOLONIO en su obra "De Sectione Rationis", obra perdida y restablecida en parte por HALLEY. Julius Petersen. Méthodes et théories pour la résolution des problèmes de constructions géométriques. Gauthier-Villars. Paris (1880); PROBLÈME 363.Enunciado auxiliar Se dan dos rectas, sobre cada una de ellas un punto, A y B, y un punto exterior P. Trazar por P una recta que encuentra a las rectas dadas en X e Y de tal manera que los segmentos AX y BY estén en una razón dada. Se determina el centro de rotación O de las rectas dadas, considerando A y B, al igual que X e Y, como puntos homólogos. La razón dada es la razón de semejanza. Como entonces OXY es semejante a OAB la recta OP será vista desde X bajo un ángulo conocido en consecuencia X se determina fácilmente.

TERCER PROBLEMA

Este problema fue propuesto y resuelto por NEWTON en la sección V del primer libro de su obra: PHILOSOPHIÆ NATURALIS PRINCIPIA MATHEMATICA Lemma XXVI *Trianguli fpecie & magnitudine dati tres angulos ad rectas totidem pofitione datas, quæ non funt omnes parallelæ, fingulos ad fingulas ponere.* Corolarium Hinc recta duci poteft cujus partes longitudine datæ rectis tribus pofitione datis interjacebunt. Concipe Triangulum DEF, puncto D ad latus EF accedente, & lateribus DE, DF in directum pofitis, mutari in lineam rectam, cujus pars data DE, rectis pofitione datis AB, AC, & pars data DF rectis pofitione datis AB, BC interponi debet; & applicando conftructionem præcedentem ad hunc cafum folvetur Problema. LemaXXVI *Situar uno a uno los tres ángulos de un triángulo de especie y magnitud dadas sobre tres rectas dadas también en posición y que no sean entre sí paralelas ninguna.* Corolario Ahora puede trazarse una recta cuyas partes de longitud dada queden interceptadas entre tres rectas de posición dada. Supongamos el triángulo EDF, cuyo punto D se acerca al lado EF, y cuyos lados DE, DF, están colocados sobre una recta, convirtiéndose en una línea recta cuya parte dada DE estará interceptada por las rectas de posición dada AB, BC; y aplicando la construcción precedente a este caso quedará el problema resuelto. Julius Petersen lo incluye en su obra: Julius Petersen. Méthodes et théories pour la résolution des problèmes de constructions géométriques. Gauthier-Villars. Paris (1880); PROBLÈME 377. Enunciado En un triángulo dado ABC, inscribir otro triángulo congruente a un triángulo dado. Como veremos en el apartado 0.9, un sistema de triángulos semejantes, inscritos en un triángulo dado, tiene un centro común de rotación; según eso, se inscribe en el triángulo dado un triángulo de la forma requerida y se determina el centro de rotación tratándolo como triángulo fundamental; se obtiene en consecuencia el triángulo buscado haciendo girar este triángulo; y se efectúa esta operación de la manera más simple, transformando por semejanza el triángulo fundamental trazado respecto al centro de rotación de manera que tenga el tamaño requerido; después se le hace girar alrededor de este mismo punto, hasta que los vértices caigan sobre los lados del triángulo dado. Enunciado de la aplicación del corolario Sobre tres rectas dadas, colocar una cuarta de tal manera que los dos segmentos determinados sobre esta última estén según magnitudes dadas. Este problema es un caso particular del anterior, ya que la recta buscada puede ser considerada como un triángulo de forma conocida.


0. SEMEJANZA - FUNDAMENTOS TEORICOS

Damos a continuación en NUEVE pasos una serie de ideas sobre la semejanza directa en el plano, que nos ayudan a establecer el método de solución perfilado en el enunciado de Julius Petersen.

ROTACION Dado un punto O, y un ángulo orientado θ, la transformación del plano que transforma un punto M en un punto M’ tal que recibe el nombre de rotación de centro O y ángulo θ. HOMOTECIA Dado un punto O, y una razón algebraica k, la transformación del plano que transforma un punto M en otro M’ tal que recibe el nombre de homotecia de centro O y razón k. SEMEJANZA Dado un punto O, un ángulo orientado θ y una razón algebraica k, la transformación del plano que transforma un punto M en un punto M’ tal que recibe el nombre de semejanza de centro O, ángulo θ y razón k.

0.1 Si desde un punto dado O se trazan rectas por los puntos de una curva dada Γ y si se hacen girar esas rectas un ángulo θ al rededor de O, y al mismo tiempo se las hace crecer (o disminuir) según una razón dada k, se obtiene una nueva curva Γ' como lugar geométrico de los extremos de las rectas que así se han hecho girar. 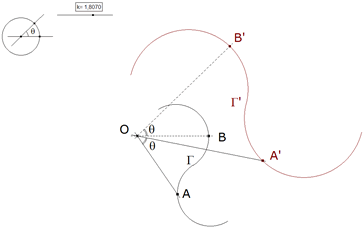figura 1 Esta nueva curva debe ser semejante a Γ, pues podemos imaginar realizadas las dos operaciones del modo siguiente: En primer lugar, rotación de la curva primitiva (sólo cambia la posición). En segundo lugar, homotecia de razón k respecto a O. Un punto A de la curva Γ determinará por semejanza un punto A' de la curva Γ'. Tales puntos se denominan homólogos. Rectas homólogas son las que unen puntos homólogos, y ángulos homólogos son los formados por rectas homólogas. El punto O puede llamarse centro de semejanza (centro de rotación), θ ángulo de rotación y k la razón de semejanza. Para dos puntos homólogos cualesquiera, A' y A, el triángulo A'OA debe conservar la misma forma ya que AOA'=θ y OA'/OA=k son constantes. Entonces también podemos decir que la curva Γ' es la que describe el vértice A' de un triángulo A'OA que, todo y conservando su forma, gira en torno de su otro vértice O, mientras que el tercer vértice recorre la curva dada. Cuando se trate de expresar que se hace girar una curva en torno a O, un ángulo de rotación θ y razón k, se podrá decir que se transforma la curva por una semejanza de centro O, razón k y ángulo θ.

0.2 Todo punto del plano puede ser considerado como perteneciente a uno de los dos sistemas (original y transformado); y en consecuencia tendrá su homólogo en el otro. Considerado el centro de rotación desde este punto de vista, será su propio homólogo (punto que se corresponde a sí mismo) y a causa de ello podemos denominarlo también el punto doble de la transformación. Igualmente se puede imaginar que todo el plano gira en torno a O de tal manera que uno de sus puntos recorre une curva dada. Si el sistema completo de puntos del plano conserva su forma durante el movimiento, uno cualquiera de sus puntos describirá una curva semejante a la curva dada.

0.3 En el momento en que se conoce el centro de rotación, el ángulo y la razón, se puede hacer girar un sistema cualquiera compuesto de rectas y arcos de círculo empleando solamente regla y compás. Se hará girar un punto A alrededor de O tomando AOA’ igual al ángulo de rotación y haciendo OA’=kOA. 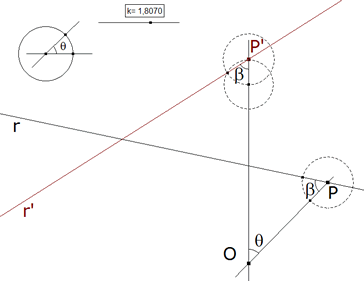figura 2 Para una recta, sólo habrá que hacer girar uno de sus puntos y trazar la recta que hará con el radio del punto nuevo un ángulo igual al que hacía la recta original con el radio del punto que se hace girar. También se pueden encontrar los homólogos de dos puntos de la recta. 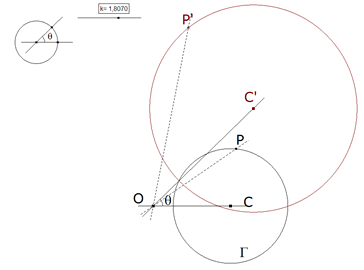figura 3 Para un círculo, bastará encontrar los homólogos de su centro y de un punto de su circunferencia.

0.4 Por medio de las proposiciones que acabamos de desarrollar, se puede resolver el problema general que sigue: ...Colocar un triángulo, semejante a un triángulo dado, de tal manera que uno de sus vértices esté en un punto dado y que los otros dos se hallen sobre dos curvas dadas... Tomamos el punto dado como centro de rotación y hacemos girar, en torno a él, una de las curvas, de manera que el ángulo de rotación sea el ángulo del triángulo cuyo vértice está en O y que la razón de semejanza sea la de los lados adyacentes a este ángulo; la curva que así se hace girar* cortará a la otra curva dada en los puntos donde debe caer el segundo vértice. Si en lugar de la forma del triángulo se conoce el ángulo cuyo vértice debe coincidir con el punto dado y el producto de los lados adyacentes a este ángulo, el problema se resuelve de la misma manera. Solamente en lugar de hacer girar una curva que se semejante a una de las curvas dadas, será su curva inversa la que se hará girar. *() En algunos casos, usamos la expresión "girar una figura hasta coincidir con la otra" como sinónimo de transformar una figura por semejanza. Espero que el contexto no ofrezca duda alguna.**

0.5 Dadas dos figuras semejantes; si sus elementos se siguen en el mismo sentido, tendrán siempre un centro de rotación, es decir un punto alrededor del cual se podrá hacer girar una de ellas para que vaya a coincidir sobre la otra; la razón de semejanza está determinada, ya que dos rectas homólogas cualesquiera están según esa razón, y el ángulo de rotación es el ángulo comprendido entre dos rectas homólogas. 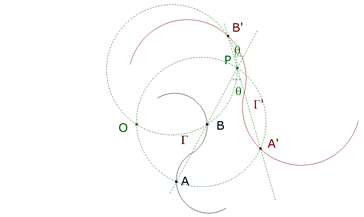figura 4 Para encontrar el centro de rotación, podríamos utilizar la razón conocida de sus distancias a un par de puntos homólogos y el arco capaz de ángulo θ para dos puntos homólogos; pero puede emplearse una construcción más simple. Sean A y A’, B y B’ dos pares de puntos homólogos. Las rectas homólogas AB y A’B’ deben comprender al ángulo de rotación; este mismo ángulo es también el que harán los radios que unen dos puntos homólogos al centro de rotación; este último debe encontrarse sobre el mismo círculo que el punto de intersección de dos rectas homólogas y de dos puntos homólogos situados sobre estas rectas. El centro de rotación de dos rectas homólogas, en dos figuras semejantes, es el centro de rotación de las propias figuras; pues si se hace girar* una recta de manera que coincida con la otra, una de las figuras deberá también coincidir con la otra. El centro de rotación de dos rectas que se extienden hasta el infinito, consideradas como figuras semejantes, está completamente indeterminado; si sobre las rectas se eligen dos puntos como homólogos, se tiene un círculo como lugar geométrico de los centros de rotación; si se dan otros dos puntos homólogos más o, lo que es lo mismo, la razón de semejanza, el centro de rotación estará completamente determinado; y es único, ya que los círculos se cortan en un segundo punto, el de intersección de las rectas. 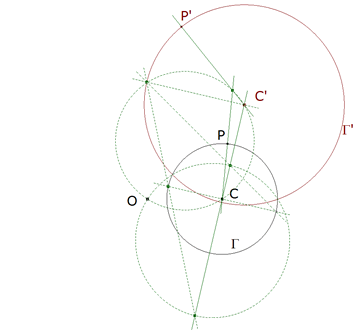figura 5 Para dos círculos, el centro de rotación es indeterminado, ya que dos cualesquiera de sus puntos pueden considerarse como puntos homólogos; como las distancias del centro de rotación a los centros de los círculos deben estar entre ellas como los radios, el lugar geométrico de este centro será un círculo que divide armónicamente la recta de centros siguiendo esa razón (es el círculo que pasa por los centros de semejanza de los dos círculos dados y tiene sus centro sobre la recta de centros). Si se eligen dos puntos de los círculos como puntos homólogos, el centro de rotación está determinado y se encuentra de la manera más simple con la ayuda de radios homólogos, ya que los centros son siempre puntos homólogos.

0.6 El centro de rotación de dos lados opuestos de un cuadrilátero es también el centro de rotación de los otros dos. 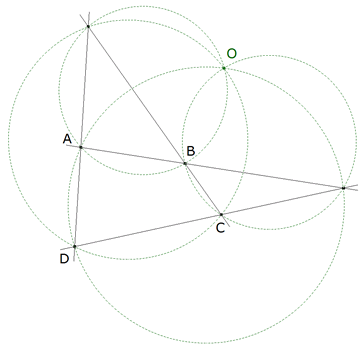figura 6 Sea O el centro de rotación de BA y CD; entonces AOB es semejante a DOC; pero se deduce fácilmente que AOD es semejante a BOC, y resulta además que O es el centro de rotación de AD y BC. En el primer caso B y C, A y D son puntos homólogos; en el segundo lo son B y A, C y D. Del mismo modo se ve que el centro de rotación de AB y CD es también el de AC y BD. Prolongamos los lados opuestos hasta que se encuentren; los círculos que determinan el centro de rotación están circunscritos a los cuatro triángulos formados en la figura; se deben utilizar los mismos círculos para determinar el centro de rotación de dos elementos cualesquiera de la figura que no se corten en uno de sus extremos; se tiene así el siguiente teorema: ...En un cuadrilátero completo, los círculos circunscritos a los triángulos que se forman, no considerando sucesivamente uno de los lados, pasan por el mismo punto, y este punto es el centro de rotación de dos segmentos cualesquiera de la figura que no se corten en uno de sus extremos...

0.7 Si se dividen según la misma razón las rectas que unen los puntos homólogos de curvas semejantes, el lugar geométrico de los puntos de división será una curva semejante a las curvas dadas, y dos cualesquiera de esas curvas tienen el mismo centro de rotación que las primeras. 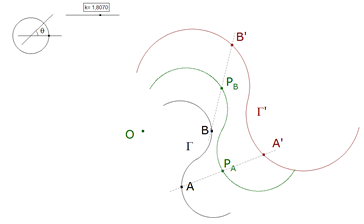figura 7 Sean A’ y A dos puntos homólogos y supongamos la recta A’A dividida por el punto P según una razón dada. Sea O el centro de rotación; la forma del triángulo A’OA debe permanecer constante; y lo mismo para AOP y en consecuencia P debe describir una curva semejante a las curvas dadas, cuando el triángulo gira alrededor de O. Corolario: Si en un cuadrilátero se trazan dos sistemas de líneas que dividen los dos pares de lados opuestos en partes proporcionales, las líneas de un mismo sistema se dividirán según la misma razón.

0.8 Si tenemos tres sistemas semejantes A, B y C y si un punto O es el centro de rotación de A y B, al mismo tiempo de B y C, debe ser también el centro de rotación de A y C. Este punto es pues el centro común de rotación de los tres sistemas; y naturalmente lo puede ser también para un número cualquiera de sistemas. 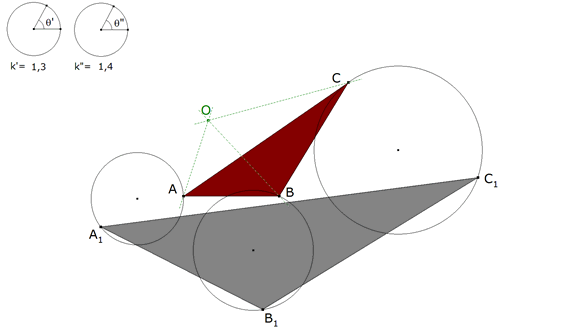figura 8 Si unimos tres puntos homólogos A, B y C de los tres sistemas con centro de rotación en O, las razones de estas rectas y los ángulos que hacen entre ellas son constantes; resulta que la forma del triángulo ABC es también constante y, por ello, lo denominaremos el triángulo fundamental. Del mismo modo, vemos que a varias figuras semejantes, que tienen un centro común de rotación, corresponde un polígono fundamental de forma constante. Si gira alrededor del centro de rotación de manera que un vértice describe une de las figuras, los otros vértices describirán las otras figuras y cualquier otro punto del plano, considerado como perteneciente al polígono fundamental, trazará una figura semejante a las otras. Como el polígono fundamental llega a tomar sucesivamente todas sus posiciones, el centro de rotación de las figuras dadas es también el centro de rotación del polígono fundamental en todas sus posiciones.

0.9 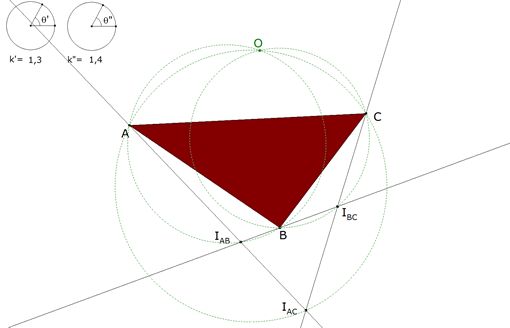figura 9 Para dos rectas, sobre las que se dan dos puntos como puntos homólogos, el centro de rotación debe encontrarse sobre un círculo que pasa por los dos puntos y el punto de intersección de las rectas dadas; para tres rectas, sobre las que se dan tres puntos como puntos homólogos, el centro de rotación está entonces determinado; es el punto de intersección de dos círculos del mismo tipo; El tercer círculo debe pasar por el mismo punto. Uniendo los tres puntos, se forma el triángulo fundamental; puede pues tener una forma cualquiera ya que se pueden elegir arbitrariamente los tres puntos; pero a los distintos triángulos fundamentales les corresponde distintos centros de rotación. Se puede determinar fácilmente el centro de rotación para un triángulo fundamental dado construyendo sobre las tres rectas un triángulo semejante al triángulo dado y determinando de esta manera tres puntos homólogos. Si las tres rectas pasan por un mismo punto O, este último será el centro de rotación para cada triángulo fundamental, de manera que los triángulos semejantes a un triángulo fundamental dado son semejantes y tienen a O por centro de semejanza. Hay no obstante un caso particular donde el centro de rotación está indeterminado; en efecto, si los vértices A y B del triángulo recorren AO y BO y si ∠C=∠AOB, C recorrerá una recta que pasa por O.


1. PRIMER PROBLEMA

Colocar un triángulo equilátero, de tal manera que sus vértices estén sobre tres rectas paralelas dadas. Uno de los vértices puede colocarse en cualquiera de las rectas; éste será el centro de rotación; el ángulo de giro será de 60º y la razón de homotecia 1.

1.1 EL PROBLEMA GENERAL

Dado un triángulo inicial O_iP_iQ_i, trazar un triángulo semejante al inicial y cuyos tres vértices reposen en tres curvas dadas: O en C₁, P en C₂ y Q en C₃.

1.1.1 REVISION DEL PROBLEMA GENERAL 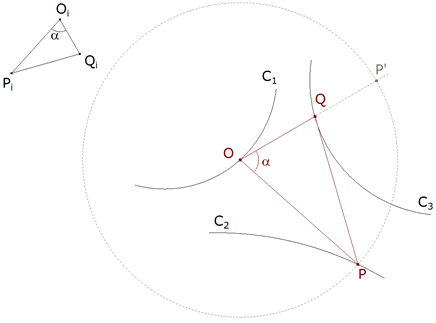figura 10 Abordamos el problema con un método útil conocido por todos: SUPONER QUE TENEMOS EL PROBLEMA RESUELTO (figura 10). Fijado O en un punto arbitrario de C₁, ¿Qué relación existe entre P y Q? Si con centro O rotamos P un ángulo α, P pasa a ocupar la posición P’ que está sobre OQ Hecha la rotación anterior, llevamos P' hasta Q, con una homotecia de centro O y razón k Pero el triángulo OPQ debe ser semejante al triángulo inicial O_iP_iQ_i, de donde 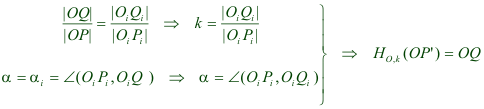Hemos deducido que fijado O, pasamos del vértice P al vértice Q por medio de una rotación de ángulo α_i=∠(O_iP_i,O_iQ_i) y centro O y seguido de una homotecia de razón k=\|O_iQ_i\|:\|O_iP_i\|.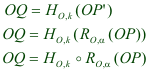

1.1.2 SOLUCION DEL PROBLEMA GENERAL Hasta aquí todo está muy bien; pero aunque sabemos donde está O (lo colocamos arbitrariamente en C₁) y conocemos la transformación que liga P y Q, ¡NO SABEMOS DONDE ESTA P! Para saberlo no queda más remedio que seguir observando la figura 11 que sigue 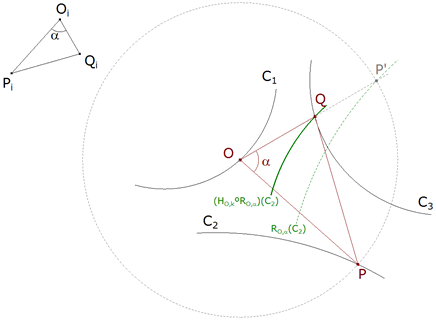figura 11 Imaginemos que al hacer la transformación del punto P, transformamos también la curva C₂. Con la rotación obtenemos y con la homotecia llegamos a Como la misma transformación transforma P en Q, C₂ acompañará a P hasta Q; pero Q según el enunciado está en C₃ y por tanto Q estará en la intersección de la transformada de C₂ y C₃ Tenemos entonces OQ y gracias a la semejanza con el triángulo inicial hallamos P y por lo tanto hemos resuelto el problema general enunciado en este apartado.

1.2 IDENTIFICACION DE NUESTRO PROBLEMA CON EL CASO GENERAL

1.2.1 ENUNCIADO Nuestro enunciado tiene un triángulo que es equilátero Nuestro enunciado tiene como curvas las tres paralelas dadas r, s, t y si inscribimos un triángulo equilátero con un vértice en cada recta, si O está en r, el vértice P está en s y el vértice Q está en t; de aquí Como el triángulo es equilátero, los lados son iguales y por tanto La transformación en nuestro problema se limita a giros de ±π/3 en torno a O. 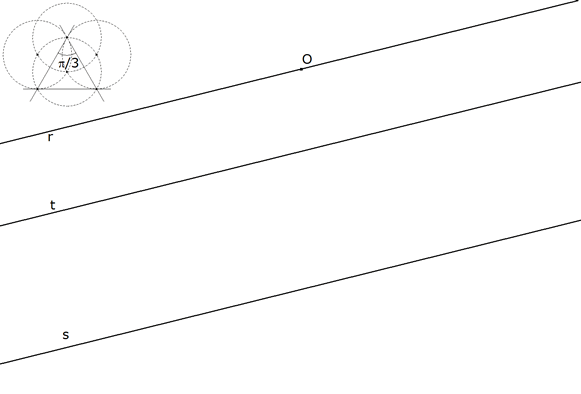figura 12 Fijamos O, un punto cualquiera sobre la recta r. (Primer vértice)

1.2.2 PRIMERA ROTACION 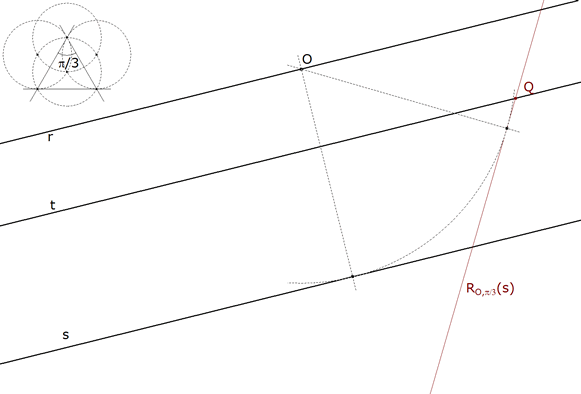figura 13 Con centro O, rotamos +π/3 la recta s. La recta rotada corta a t en Q (segundo vértice). Podemos hacer la rotación con regla y compás o usar CABRI que implementa la rotación con centro en un punto.

1.2.3 SEGUNDA ROTACION Sabiendo que el triángulo es equilátero sería fácil hallar el punto P; pero al fin y al cabo y siguiendo el razonamiento general P sería el transformado de Q por la transformación inversa. 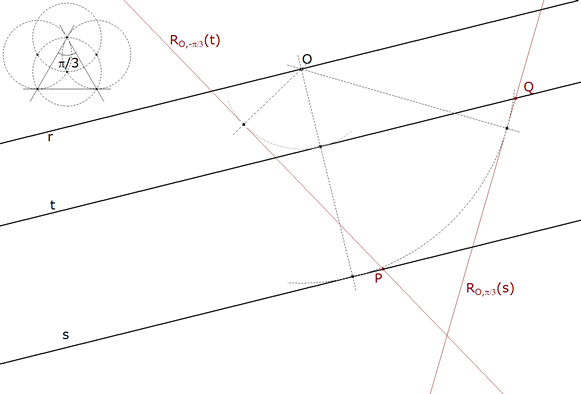figura 14 Con centro O, rotamos -π/3 la recta t. La recta rotada corta a s en P (tercer vértice).

1.2.4 LA PRIMERA SOLUCION 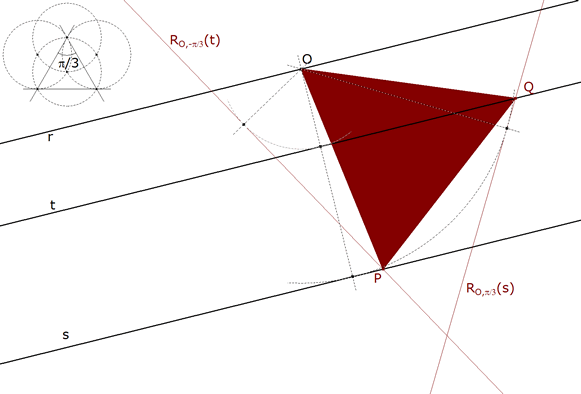figura 15 OPQ es el triángulo buscado.

1.2.5 LA SEGUNDA SOLUCION 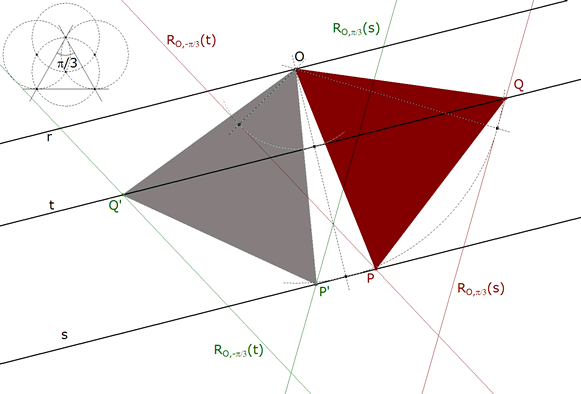figura 16 Repitiendo el proceso anterior girando en sentido contrario obtenemos O'P'Q' que también es solución.

1.3 LAS INDICACIONES DE JUAN SAPIÑA

1.3.1 PLANTEAMIENTO 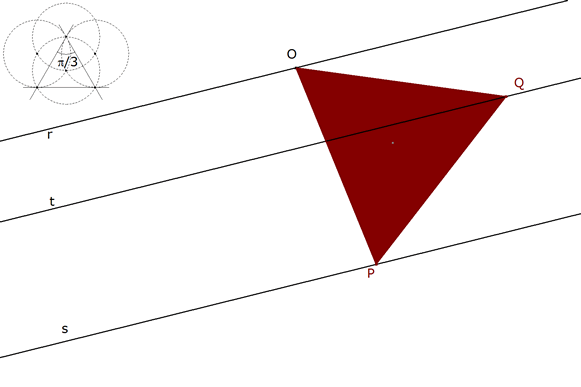figura 17 Repetimos el método de: SUPONER QUE TENEMOS EL PROBLEMA RESUELTO (figura 17).

1.3.2 OBSERVACION DE LA FIGURA 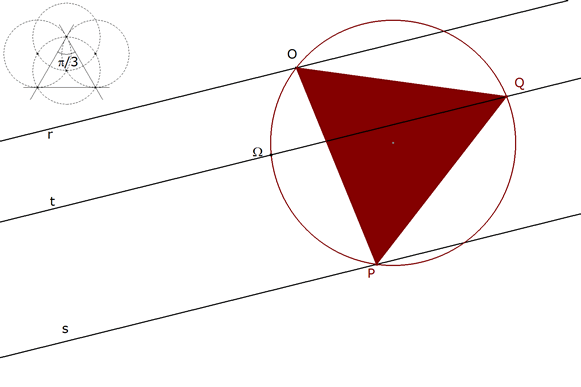figura 18 Si trazamos el círculo circunscrito al triángulo OPQ, éste vuelve a cortar la recta t en Ω.

1.3.3 EL ANGULO OΩQ 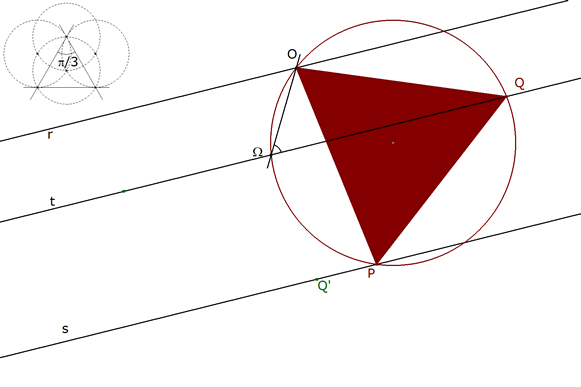figura 19 Basta observar que el ángulo OΩQ subtiende el arco OQ; pero OQ es también el ángulo que subtiende el ángulo OPQ: Pero como OPQ es solución, es equilátero y por tanto OPQ es un ángulo de π/3 y así:

1.3.4 EL ANGULO PΩQ 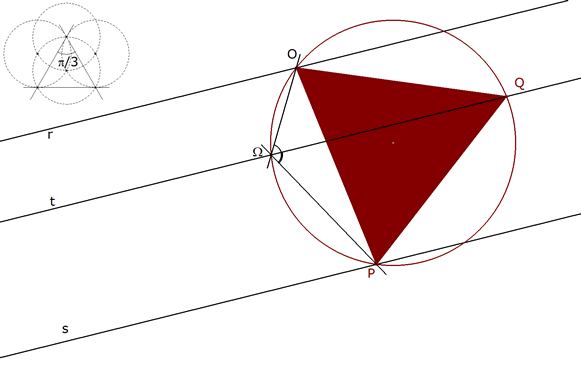figura 20 Por un razonamiento análogo al anterior:

1.3.5 LA PRIMERA SOLUCION (I) 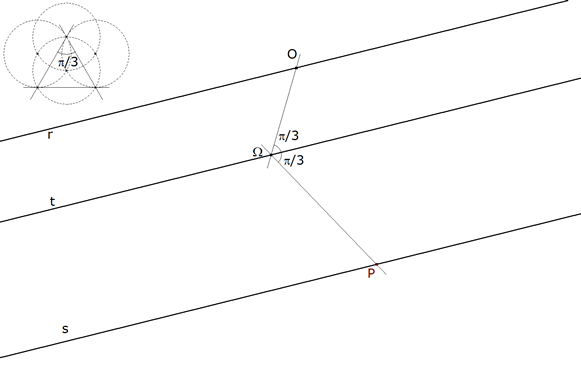figura 21 Podemos tomar un punto Ω cualquiera sobre t; pero para obtener las soluciones de 1.2 partimos del punto O anterior. La recta por O que forma un ángulo de π/3 con t corta en Ω a t. La otra recta por Ω que forma un ángulo de π/3 con t corta a s en P.

1.3.6 LA PRIMERA SOLUCION (II) 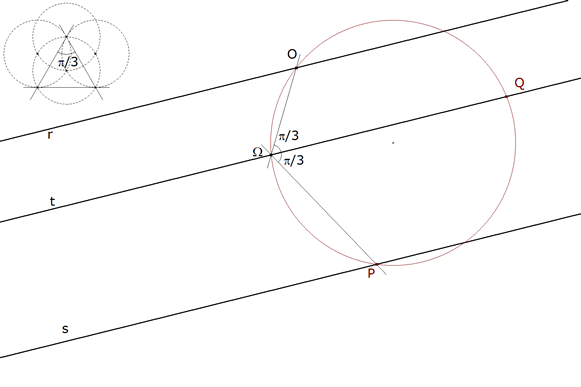figura 22 El círculo circunscrito a OΩP vuelve a cortar a t en Q.

1.3.7 LA PRIMERA SOLUCION y (III) 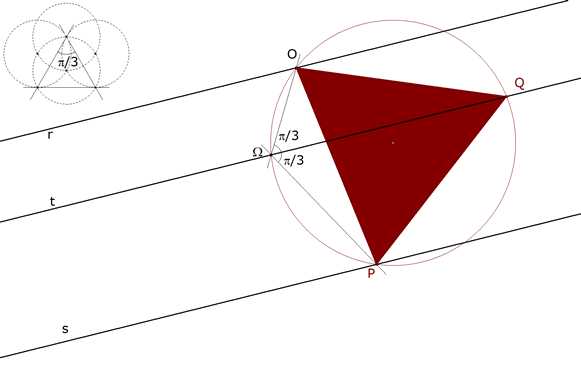figura 23 OPQ es el triángulo buscado.

1.3.8 LA SEGUNDA SOLUCION 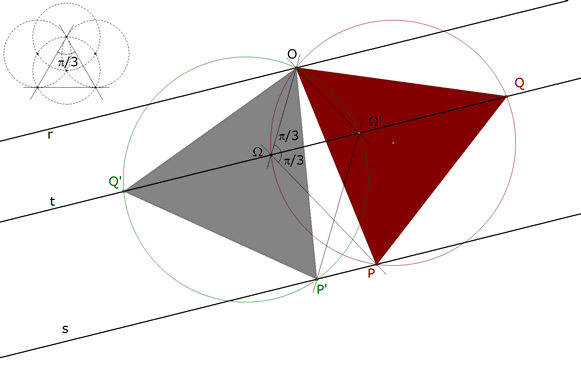figura 24 La otra recta por O que forma un ángulo de π/3 con t corta en Ω' a t. La otra recta por Ω’ que forma un ángulo de π/3 con t corta a s en P’. El círculo circunscrito a OΩ’P’ vuelve a cortar a t en Q’. OP’Q’ es el otro de los triángulos buscados.


2. SEGUNDO PROBLEMA

2.1 EL PROBLEMA AUXILIAR

Se dan dos rectas, sobre cada una de ellas sendos puntos, A y B, y además un punto exterior P. Trazar por P una recta que encuentre a las rectas dadas en X e Y de tal manera que los segmentos AX y BY estén según una razón dada. Se determina el centro de rotación O de las rectas dadas, considerando A y B, al igual que X e Y, como puntos homólogos. La razón dada es la razón de semejanza. Como entonces OXY es semejante a OAB la recta OP será vista desde X bajo un ángulo conocido; en consecuencia X se determina fácilmente.

2.1.1 DATOS DEL ENUNCIADO 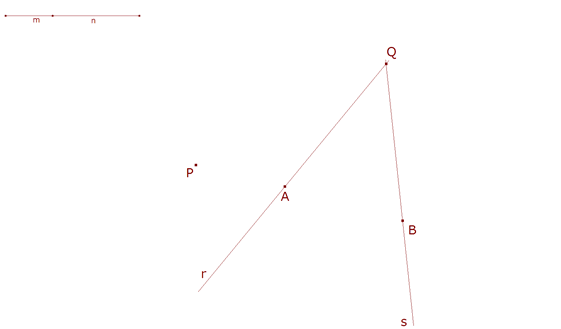figura 25 dibujamos el enunciado.

2.1.2 PRIMERA SUGERENCIA DEL ENUNCIADO 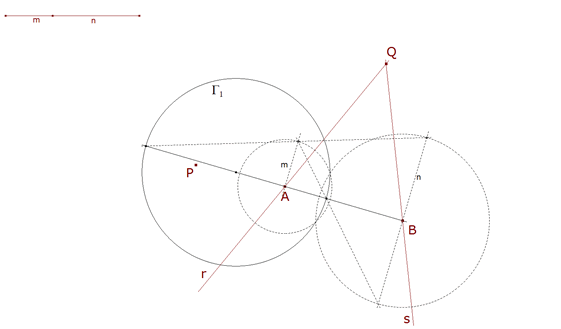figura 26 Según la indicación del enunciado: “...Se determina el centro de rotación O de las rectas dadas, considerando A y B, al igual que X e Y, como puntos homólogos. La razón dada es la razón de semejanza...” Según 0.5 (figura 5): “...Para dos círculos, el centro de rotación es indeterminado, ya que dos cualesquiera de sus puntos pueden considerarse como puntos homólogos; como las distancias del centro de rotación a los centros de los círculos deben estar entre ellas como los radios, el lugar geométrico de este centro será un círculo que divide armónicamente la recta de centros siguiendo esa razón (es el círculo que pasa por los centros de semejanza de los dos círculos dados y tiene sus centro sobre la recta de centros)...” Obtenemos el círculo Γ₁ como primer lugar que contiene al centro de rotación.

2.1.3 SEGUNDA SUGERENCIA DEL ENUNCIADO 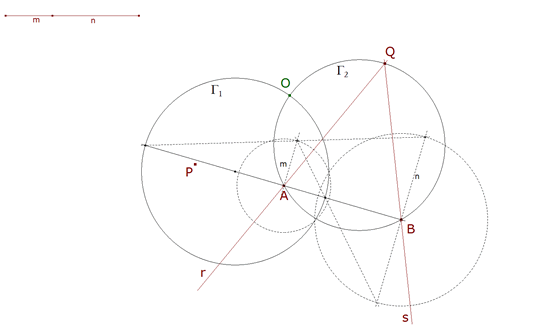figura 27 Según la indicación del enunciado: “...Se determina el centro de rotación O de las rectas dadas, considerando A y B, al igual que X e Y, como puntos homólogos...” Según 0.5 (figura 4) “...pero puede emplearse una construcción más simple. Sean A y A’, B y B’ dos pares de puntos homólogos. Las rectas homólogas AB y A’B’ deben comprender al ángulo de rotación; este mismo ángulo es también el que harán los radios que unen dos puntos homólogos al centro de rotación; este último debe encontrarse sobre el mismo círculo que el punto de intersección de dos rectas homólogas y de dos puntos homólogos situados sobre estas rectas...” Tomando A y B como homólogos y Q punto de intersección de las rectas dadas, obtenemos el círculo Γ₂ como segundo lugar que contiene al centro de rotación.

2.1.4 TERCERA SUGERENCIA DEL ENUNCIADO 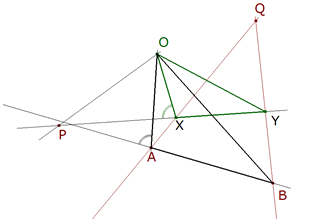figura 28 Según la indicación del enunciado: “...Como entonces OXY es semejante a OAB la recta OP será vista desde X bajo un ángulo conocido en consecuencia X se determina fácilmente...” En la figura 28 vemos la causa. Si suponemos el problema resuelto deducimos el ángulo bajo el que se ve OP desde X

2.1.5 EL ARCO CAPAZ QUE CONTIENE A X 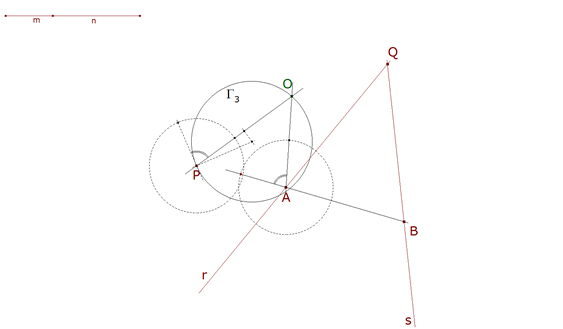figura 29 Determinamos entonces π-∠OAB y lo trasladamos como arco capaz de OP. Como desde X se ve OP bajo ese ángulo, X está sobre el círculo Γ₃ que acabamos de dibujar con el arco capaz mencionado.

2.1.6 DETERMINACION DE X 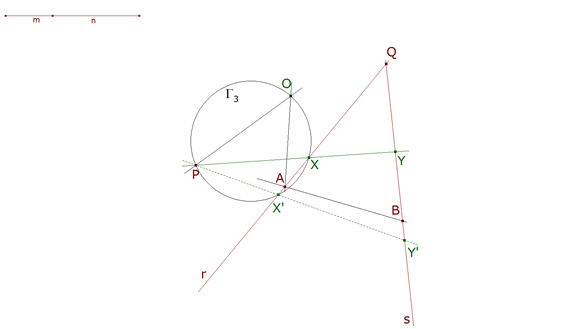figura 30 Pero X además está sobre la recta r=AQ, entonces y a lo sumo puede haber dos soluciones pues un círculo corta a la recta en cero, uno o dos puntos. figura 31 Así queda con todas las líneas vistas.

2.2 EL PROBLEMA PRINCIPAL

Por un punto dado P, trazar una recta que forme con otras dos rectas dadas, un triángulo de área dada. Sea A el punto de intersección de las rectas dadas; se representa el área dada bajo la forma de un triángulo, del que un lado es AP y el otro está sobre una de las rectas dadas. La recta buscada debe ser tal que el elemento de área que se añade al triángulo sea igual al que determina la sección en el triángulo. Pero esas dos áreas son triángulos cuyas alturas son conocidas. La razón de las bases de esos triángulos es pues conocida también y en consecuencia, el problema se transforma en el problema auxiliar anterior.

2.2.1 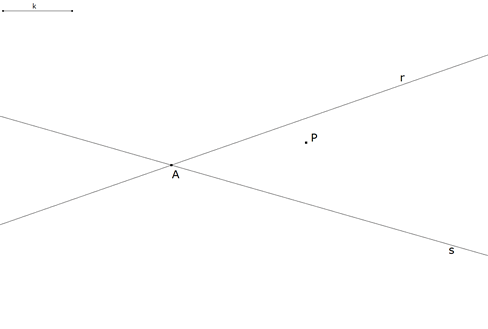figura 32 Dibujamos el enunciado.

2.2.2 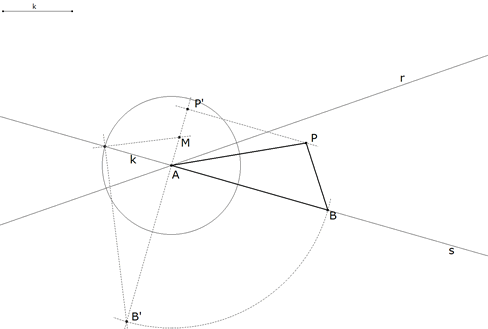figura 33 Según la indicación del enunciado: “... Sea A el punto de intersección de las rectas dadas; se representa el área dada bajo la forma de un triángulo, del que un lado es AP y el otro está sobre una de las rectas dadas ...” Es decir dado un segmento k hallar B sobre s tal que Sea M el punto medio de P’A. Por P una paralela a s y por A una perpendicular a s determinan P’. La perpendicular a la recta, que une M con la intersección de s y el círculo de centro A y radio k, corta a P’A en B’. AB’ es la base del triángulo buscado y PS su altura. Llevamos AB’ sobre s y determinamos B.

2.2.3 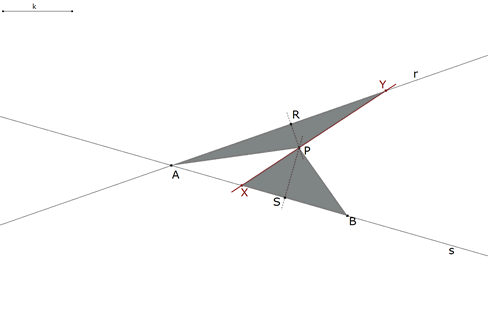figura 34 Según la indicación del enunciado: “... La recta buscada debe ser tal que el elemento de área que se añade al triángulo sea igual al que determina la sección en el triángulo. Pero esas dos áreas son triángulos cuyas alturas son conocidas. La razón de las bases de esos triángulos es pues conocida también y en consecuencia, el problema se transforma en el problema auxiliar ...” Supongamos para ello que tenemos el problema resuelto, entonces En la última relación es fácil ver el problema auxiliar donde la razón dada es la razón de las distancias del punto P a las rectas dadas. Sigamos pues con el procedimiento desarrollado en el problema auxiliar.

2.2.4 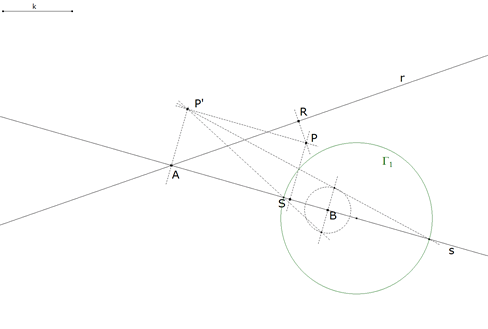figura 35 Para determinar el centro de giro, como hemos visto en 2.1.2 (figura 26), trazamos el círculo de Apolonio para los puntos B y A con razón de distancias Tenemos el círculo Γ₁ como primer lugar geométrico que contiene al centro de giro.

2.2.5 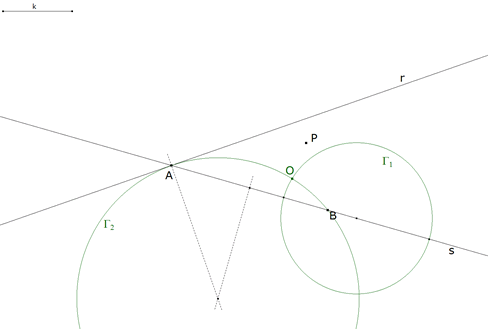figura 36 Como hemos visto en 2.1.3 (figura 27), trazamos el círculo que pasa por los puntos B, A y la intersección de las rectas dadas; pero A es ese punto, entonces como B y A son puntos de s, considerando A también como punto de r, resulta que el círculo será tangente a r en A. La mediatriz de BA y una perpendicular a r en A determinan el centro del círculo buscado. Tenemos el círculo Γ₂ como segundo lugar geométrico que contiene al centro de giro

2.2.6 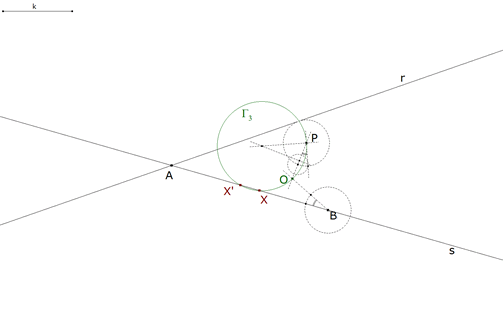figura 37 Como hemos visto en 2.1.5 (figura 29), determinamos el ángulo OBA. Trazamos ahora el arco capaz del ángulo OBA y segmento OP. Tenemos el círculo Γ₃ como lugar geométrico de los puntos X que se ven desde OP bajo un ángulo OBA. Pero X además está sobre la recta s=AB, entonces

2.2.7 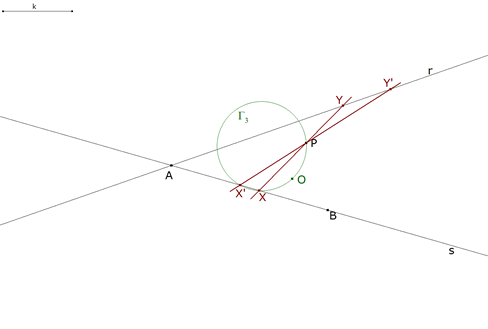figura 38 La recta XP que corta a la recta s en Y y la recta X’P que corta a s en Y’ son las soluciones pedidas.

2.3 LA SOLUCION DE JUAN SAPIÑA BORJA

Exponemos ahora una solución completamente distinta que Juan Sapiña, su autor, denomina método de isogonales. La solución de su libro no contempla los pasos constructivos intermedios (figuras 40, 41, 42). CEVIANAS ISOGONALES Dos rectas que parten del vértice de un ángulo se llaman isogonales, respecto a los lados del mismo; cuando forman con ellos ángulos iguales, es decir; cuando son simétricas respecto a la bisectriz del ángulo considerado.

2.3.1 PLANTEO 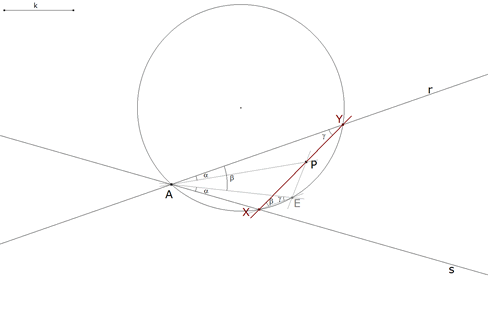figura 39 Supuesto el problema resuelto, trazamos PA que forma un ángulo α con AY. Trazamos la recta que forma un ángulo α con AX y corta al círculo circunscrito AXY en E. Entonces los triángulos YAP y XEA son semejantes por la igualdad de los ángulos γ Que es una propiedad de las isogonales. Como conocemos el ángulo A y el área podemos escribir todos son valores conocidos y además (figura 39)

2.3.2 CONSTRUCCION 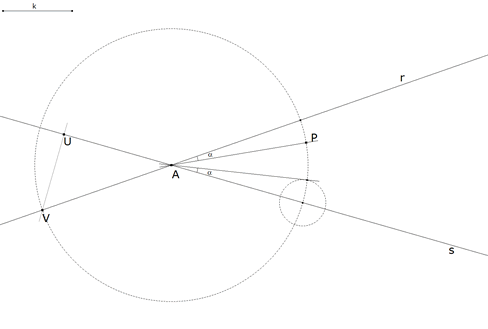figura 40 Llevamos el ángulo α desde A sobre la recta s; además

2.3.3 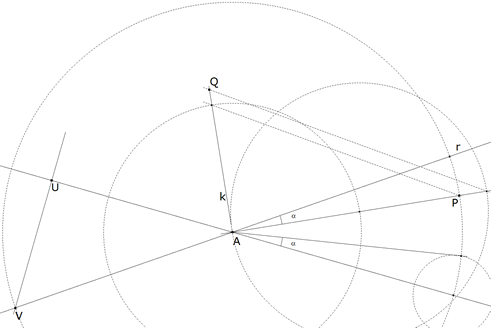figura 41 Trazamos ahora AQ que nos permite trazar AE 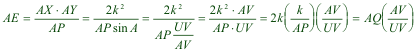Basta dibujar (ver figura 41)

2.3.4 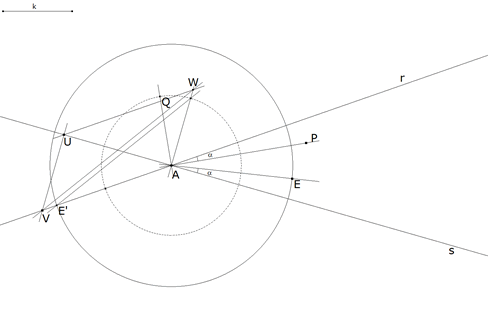figura 42 Acabamos de trazar AE haciendo Por A paralela a UV y por U paralela a AV determinan W tal que UV=AW paralela a VW por la intersección de AW y del círculo de radio AQ; esta paralela corta a AV en E’ tal que AE’=AE.

2.3.5 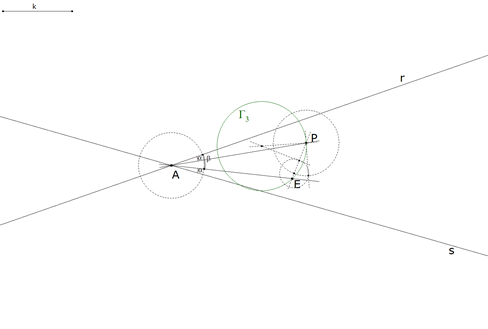figura 43 Sobre PE trazamos el arco capaz de ángulo Obtenemos el círculo Γ₃ lugar geométrico de los puntos X desde los que se ve PE bajo un ángulo β. ¡Es el mismo círculo Γ₃ hallado en 2.2.5 (figuras 37 y 38)

2.3.6 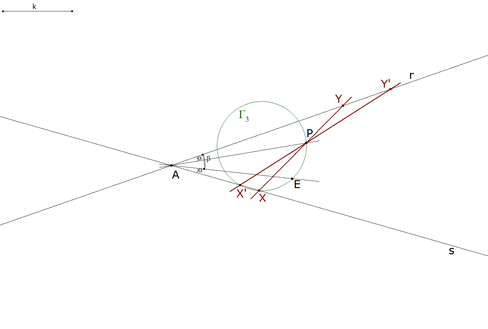figura 44 Pero X además está sobre la recta s, entonces La recta XP que corta a la recta s en Y y la recta X’P que corta a s en Y’ son las soluciones pedidas.

2.4 LA SOLUCION DE GEORGES RITT

Generalmente, hacemos un planteamiento geométrico, la complementamos con alguna manipulación algebraica y concluimos la construcción geométrica que resuelve el problema. El atractivo es, en este caso, que de un planteamiento puramente algebraico deducimos el método geométrico. Para la solución tomamos las rectas dadas como ejes de coordenadas; por tanto trabajamos en ejes oblicuos.

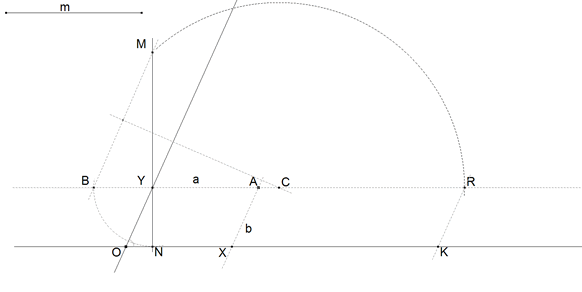
2.4.1 PLANTEAMIENTO 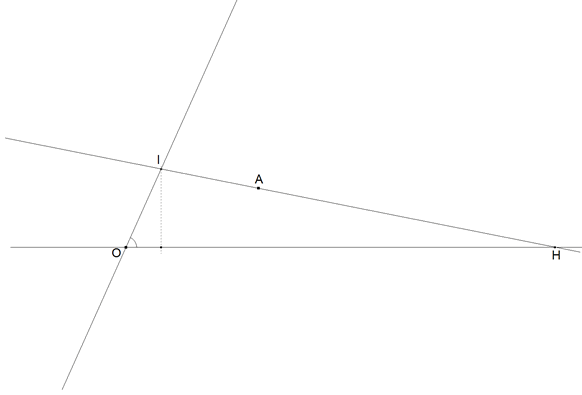figura 45 Damos dos rectas que se cortan en un punto O y damos un punto cualquiera A, una recta por A corta a las rectas dadas en H e I respectivamente (ver figura 45). Las rectas dadas y la recta por A forman un triángulo OIH. El área de este triángulo es un valor dado (por ejemplo m²)

2.4.2 LOS DATOS 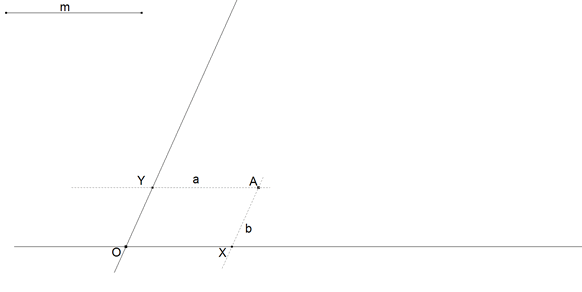figura 46 Tomamos las rectas dadas como ejes de coordenadas oblicuos (no rectangulares). Trazamos por A paralelas a los ejes establecidos. En estos ejes podemos escribir De acuerdo con la figura 45, tomamos por ejemplo y observando la figura 45, de nuevo, escribimos la recta IAH como que para x=0 nos da Con las expresiones de H e I entramos en la ecuación del área del triángulo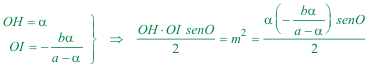

2.4.3 EL CAMBIO DE UN CUADRADO A UN PARALELOGRAMO EQUIVALENTE figura 47 Para simplificar el resultado anterior, hacemos el cambio geométricamente, este cambio significa transformar el cuadrado de lado m por un paralelogramo OYRK de idéntica área de lados Ahora, por Y, una perpendicular a OX sobre la que, con el compás, trazamos M. YM corta a OX en N después, por Y, una paralela a OX. Con centro en Y, un arco de radio YN que corta a la paralela en B. La mediatriz de BM corta a BY en C. El arco de centro C y radio CM corta a BY en R. Una paralela por R a OY corta a OX en K. BR es el diámetro del círculo con centro en C que pasa por M; ya que Como CM es perpendicular al diámetro Por lo tanto OYRK es el paralelogramo de lados b y k con igual área que el cuadrado de lado m. Lo anterior nos lleva a cuyas soluciones son

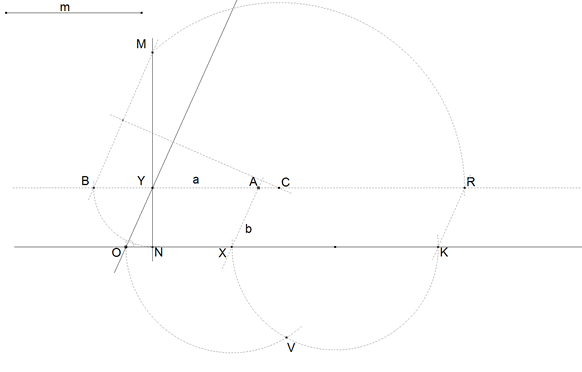2.4.4 HALLAR figura 48 Semicírculo de diámetro KX Con centro en X, un arco de radio XO que corta al semicírculo anterior en V. Por estar sobre el semicírculo

2.4.5 AHORA H (OH=α) 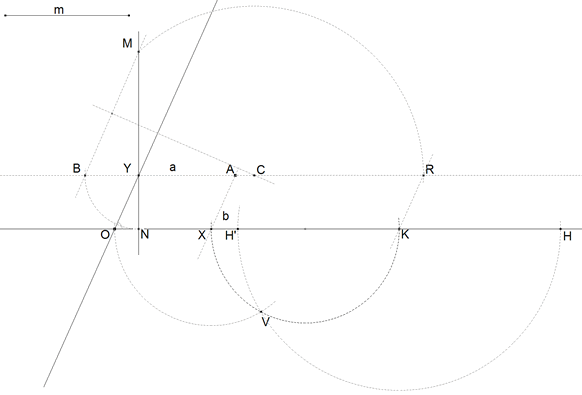figura 49 Con centro K y radio KV arco que corta a OX en H y H'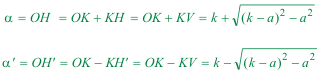

2.4.6 LA PRIMERA SOLUCIÓN 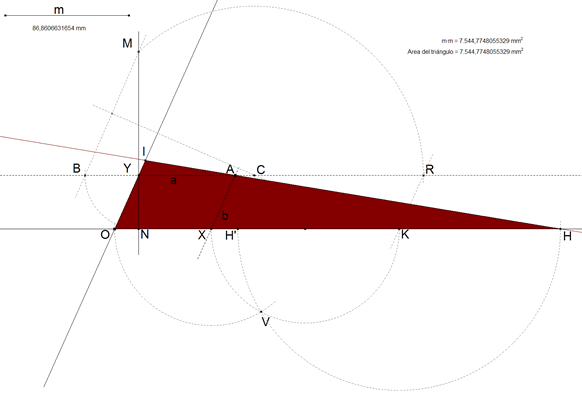figura 50 Una recta por H y A corta a OY en I. OIH es un triángulo de área m².

2.4.7 LA SEGUNDA SOLUCIÓN 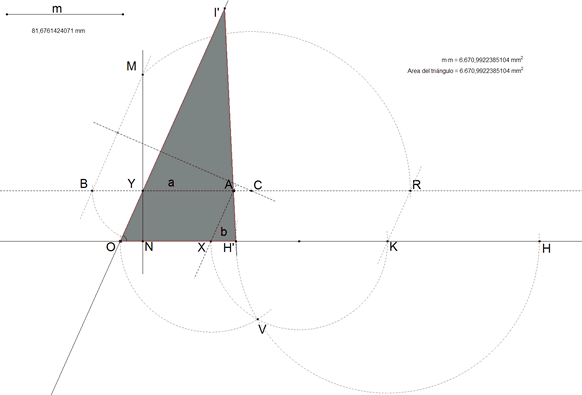figura 51 Una recta por H' y A corta a OY en I'. OI'H' es un triángulo de área m².

2.4.8 CONCLUSIONES Se obtienen dos soluciones siempre que pero sólo hay una solución si y no hay ninguna solución si

2.5 LA SOLUCION DE NICOLAS ROSILLO

Presentamos, a continuación, una solución entermanete analítica presentada por Nicolás Rosillo al problema 256 de TRIANGULOSCABRI (RICARDO BARROSO CAMPOS).

2.5.1 PLANTEAMIENTO Adoptamos un sistema de coordenadas rectangular en el que el punto dado se toma como origen que notamos O. El eje de ordenadas se toma paralelo a la primera recta dada. El eje de abscisas será la perpendicular al eje de ordenadas por el origen. 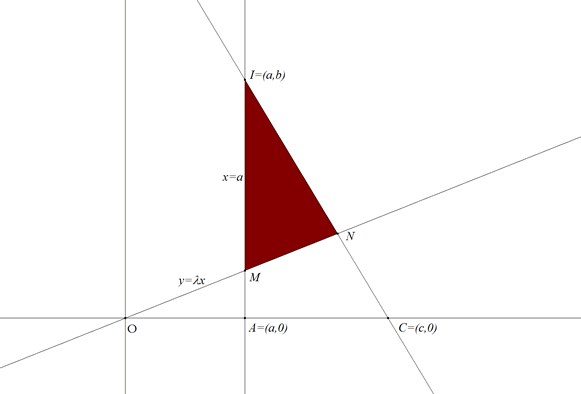figura 52 Si consideramos el punto de intersección I de las rectas dadas como el punto de coordenadas (a,b); la primera recta será la recta que pasa por A=(a,0) e I=(a,b); la segunda recta será la recta que pasa por C=(c,0) e I=(a,b). La recta buscada pasa por el origen y es de la forma Imponemos la condición de que el área del triángulo formado por las dos rectas dadas y esta recta variable por el origen sea igual a m².

2.5.2 RESOLUCIÓN El primer vértice del triángulo buscado es I y es un dato La primera recta dada pasa por los puntos I y A, tiene por ecuación La segunda recta dada es la recta que pasa por los puntos I y C, tiene por ecuación El segundo vértice del triángulo es el punto M El tercer vértice del triángulo es el punto N 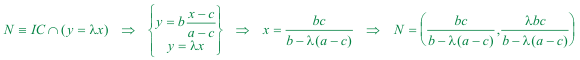Imponemos la condición de que el área del triángulo de vértices I, M, N es igual a m². 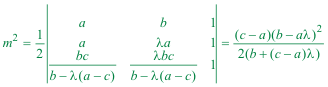De donde despejamos λ y obtenemos dos valores Que podemos construir geométricamente; pero de modo más laborioso que el que proporciona la solución de Georges Ritt.


3. TERCER PROBLEMA

3.1 LA SOLUCION DE ISAAC NEWTON

*Situar uno a uno los tres ángulos de un triángulo de especie y magnitud dadas sobre tres rectas dadas también en posición y que no sean entre sí paralelas ninguna.* Exponemos ahora la solución que Isaac Newton presenta en el Lema XXVI de PHILOSOPHIÆ NATURALIS PRINCIPIA MATHEMATICA.

3.1.1 PHILOSOPHIÆ NATURALIS PRINCIPIA MATHEMATICA, EDICION DE 5 DE JULIO DE 1686 figura 53 figura 54 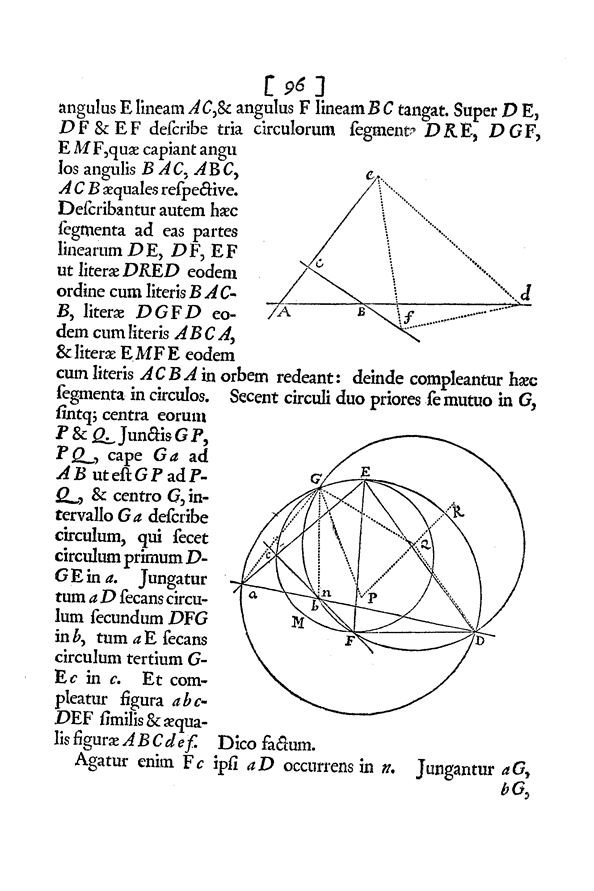figura 55 figura 56

3.1.2 EJECUCION LEMA XXVI Situar uno a uno los tres ángulos de un triángulo de especie y magnitud dadas sobre tres rectas dadas también en posición y que no sean entre sí paralelas ninguna. 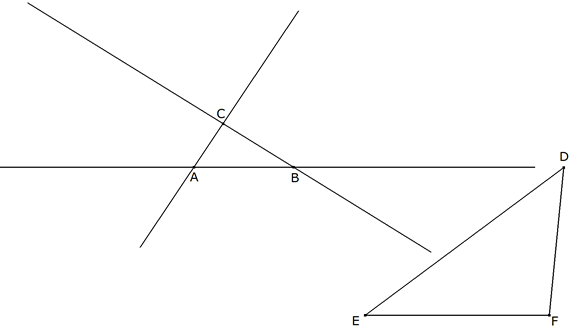figura 57 Se tienen en posición tres rectas infinitas, AB, AC, BC y es preciso colocar el triángulo DEF de tal manera... 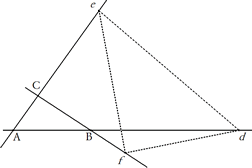figura 58 ...que su ángulo D toque la línea AB, el ángulo E toque la línea AC y el ángulo F la línea BC 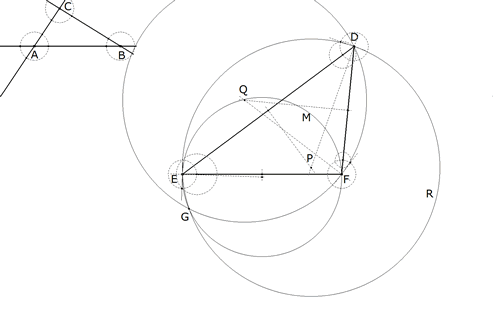figura 59 ... Sobre DE, DF y EF trácense tres segmentos circulares DRE, DGF, EMF., que comprendan ángulos respectivamente iguales a los ángulos BAC, ABC, ACB. Pero se han de trazar estos segmentos sobre aquellas partes de las líneas DE, DF, EF, de tal modo que al girar las letras DRFD lo hagan en el mismo orden que las letras BACB y que las letras DGFE giren en el mismo orden que las letras ACBA; después complétense estos segmentos circulares en sus círculos completos. Sea G el punto en que se corten los dos primeros círculos y sean sus centros P y Q. 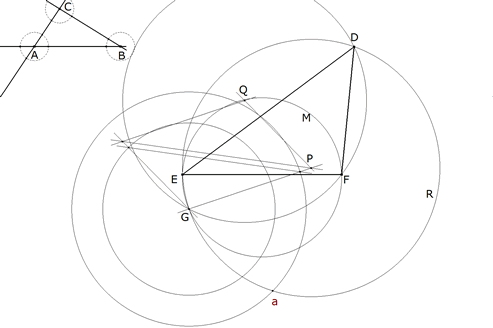figura 60 ... Unidos GP, PQ, tómese Ga a AB como GP a PQ y, con centro en G y con distancia Ga trácese un círculo que corte al círculo primero DGE en a. 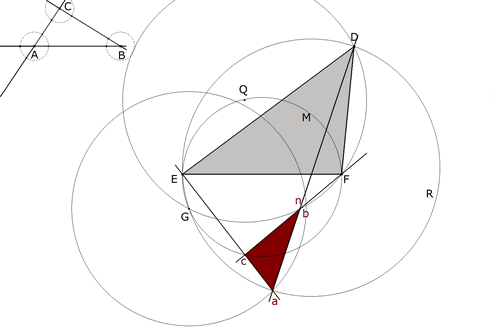figura 61 Unase por una, parte aD secante del círculo segundo DFG en b y por otra aE secante del círculo tercero EMF en c. Y ya es factible la figura ABCdef semejante e igual a la figura abcDEF. Con lo cual se completa el problema. Trácese, pues, Fc que toque a aD en n, y únanse aG, bG, QG, QD, PD. Por construcción, el ángulo EaD es igual al ángulo CAB, y el ángulo acF igual al ángulo ACB, y por tanto el triángulo anc equiángulo con el triángulo ABC. Luego el ángulo anc o FnD, es igual al ángulo ABC y por tanto al ángulo FbD, y por eso el punto n coincide con el punto b. Además, el ángulo GPQ, que es la mitad del ángulo central GPD, es igual al ángulo en la circunferencia GaD, y el ángulo GQP, que es la mitad del ángulo central GQD, es igual al complemento para dos rectos del ángulo en la circunferencia GbD y por tanto igual al ángulo Gba; y así los ángulos GPQ, Gab son semejantes; y Ga es respecto a ab como GP es a PQ; esto ^`es (por construcción) como Ga a AB. Pero son iguales ab y AB y por tanto los triángulos abc y ABC, que acabamos de probar que son semejantes, son también iguales. En consecuencia, puesto que los ángulos D, E, F, del triángulo DEF caen respectivamente sobre los lados ab, ac, bc, del triángulo abc, la figura ABCdef puede ser completada semejante e igual a la figura abcDEF, y construyéndola quedará resuelto el problema. Q.E.F. 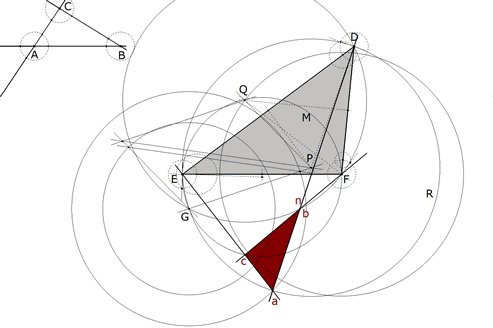figura 62 Así queda la construcción con todas sus líneas; sólo falta colocar un triángulo congruente a EDF en ABC. Corolario. Ahora puede trazarse una recta cuyas partes de longitud dada queden interceptadas entre tres rectas de posición dada. Supongamos el triángulo DEF, cuyo punto D se acerca al lado EF, y cuyos lados DE, DF, están colocados sobre una recta, convirtiéndose en una línea recta cuya parte dada DE estará interceptada por las rectas de posición dada AB, AC y la otra parte dada DF estará interceptada por las rectas de posición dada AB, BC; y aplicando la construcción precedente a este caso quedará el problema resuelto.

3.2 LAS INDICACIONES DE JULIUS PETERSEN

En un triángulo dado ABC, inscribir otro triángulo congruente a un triángulo dado. Según el apartado 0.9, un sistema de triángulos semejantes, inscritos en un triángulo dado, tiene un centro común de rotación; según eso, se inscribe en el triángulo dado un triángulo de la forma requerida y se determina el centro de rotación tratándolo como triángulo fundamental; se obtiene en consecuencia el triángulo buscado haciendo girar este triángulo; y se efectúa esta operación de la manera más simple, transformando por semejanza el triángulo fundamental trazado respecto al centro de rotación de manera que tenga el tamaño requerido; después se le hace girar alrededor de este mismo punto, hasta que los vértices caigan sobre los lados del triángulo dado.

3.2.1 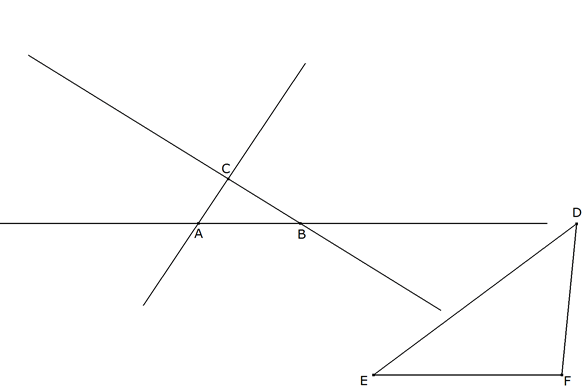figura 63 Dibujamos el enunciado. ABC el triángulo dado. DEF el otro triángulo dado de la forma requerida.

3.2.2 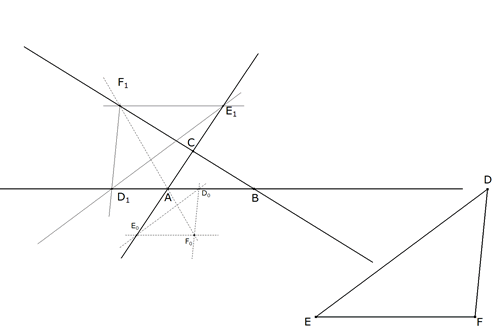figura 64 Según la indicación del enunciado: “... se inscribe en el triángulo dado un triángulo de la forma requerida ...” El homólogo de D sobre AB, el homólogo de E sobre CA y el homólogo de F sobre BC. Tomamos sobre AB un punto cualquiera D₀, por D₀ paralela a ED que corta a CA en E_0.Una paralela por E₀ a EF y una paralela por D₀ a FD se cortan en F₀. D₀E₀F₀ es homotético a DEF. Para hallar el triángulo homotético e inscrito, tomamos A como centro de esta homotecia. La recta AF₀ corta a CB en F₁. Obtenido F₁, por medio de las correspondientes paralelas a EF y a FD obtenemos E₁ sobre CA y D₁ sobre AB. D₁E₁F₁ es el triángulo homotético (con la forma requerida) inscrito en ABC. A partir de aquí determinaremos otro triángulo circunscrito y congruente con DEF.

3.2.3 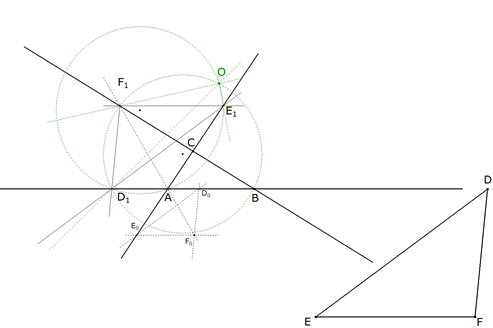figura 65 Según la indicación del enunciado: “... y se determina el centro de rotación tratándolo como triángulo fundamental; ...” Supongamos para ello que D₁E₁F₁ son puntos homólogos sobre las tres rectas dadas AB, CA y BC. Si D₁ y E₁ son homólogos, AB y CA se cortan en A; luego el centro de rotación está sobre el círculo por D₁, E₁ y A. Si F₁ y D₁ son homólogos, AB y BC se cortan en B; luego el centro de rotación está sobre el círculo por F₁, D₁ y B. O está en la intersección de los círculos hallados.

3.2.4 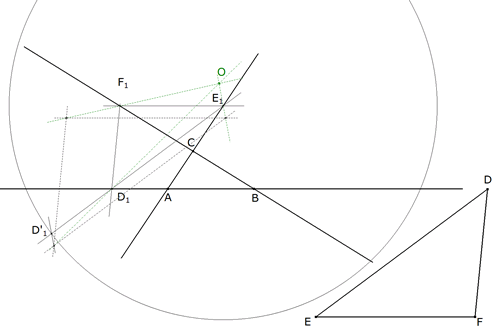figura 66 Hallamos ahora un triángulo homotético a D₁E₁F₁ respecto a O y congruente con DEF. Con centro en E₁, círculo de radio ED que corta a E₁D₁ en D’_1. Por D’₁ paralela a OE₁ que corta a OD₁ en el vértice homólogo de D₁. Las paralelas a F₁D₁ y a D₁E₁ determinan los vértices homólogos a F₁ y a E₁. Tenemos centrado en O a un triángulo idéntico a EDF (punteado en la figura 23). Ya sólo nos queda girar este último triángulo en torno a O hasta que los vértices coincidan con los lados de ABC para obtener la solución.

3.2.5 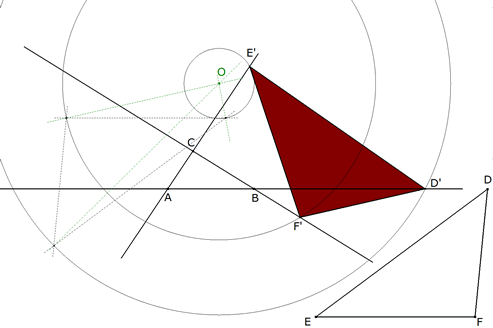figura 67 Para los giros, trazamos tres círculos con centro en O. Para el homólogo de D, el círculo pasa por el homólogo de D₁ y corta a AB por primera vez en D’. Para el homólogo de E, el círculo pasa por el homólogo de E₁ y corta a CA por primera vez en E’. Para el homólogo de F, el círculo pasa por el homólogo de F₁ y corta a BC por primera vez en F’. D’E’F’ es una de las soluciones buscadas.

3.2.6 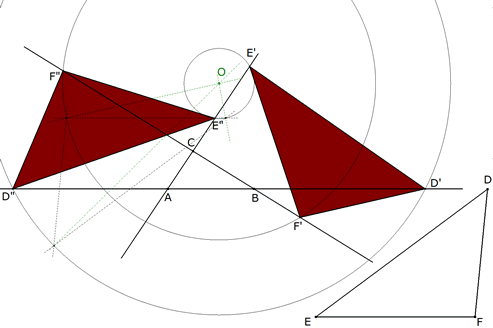figura 68 Como un círculo corta a una recta a lo sumo en dos puntos, la segunda intersección de cada círculo en su lado correspondiente nos proporciona una nueva solución.

3.2.7 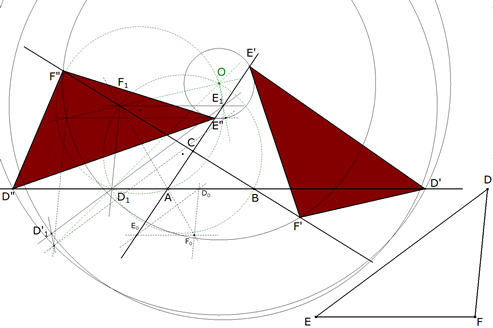figura 69 Así queda la construcción completa con todas sus líneas.

3.3 APLICACION DEL COROLARIO

Ahora puede trazarse una recta cuyas partes de longitud dada queden interceptadas entre tres rectas de posición dada. Supongamos el triángulo EDF, cuyo punto D se acerca al lado EF, y cuyos lados DE, DF, están colocados sobre una recta, convirtiéndose en una línea recta cuya parte dada DE estará interceptada por las rectas de posición dada AB, BC; y aplicando la construcción precedente a este caso quedará el problema resuelto. Sobre tres rectas dadas, colocar una cuarta de tal manera que los dos segmentos determinados sobre esta última estén según magnitudes dadas. ( Dadas u, v, w tres rectas cualesquiera, colocar entre ellas una cuarta recta r de forma que los segmentos que forman las tres rectas en r tengan longitudes dadas m, n.) Este problema es un caso particular del anterior, ya que la recta buscada puede ser considerada como un triángulo de forma conocida. En un triángulo dado ABC, inscribir otro triángulo congruente a un triángulo dado DEF. ABC es el triángulo que forman las tres rectas u, v, w. DEF más que un triángulo es un pseudo-triángulo. Tomamos DE=m y EF=n; DEF son colineales. Podemos aplicar el procedimiento visto hasta aquí.

3.3.1 ENUNCIADO 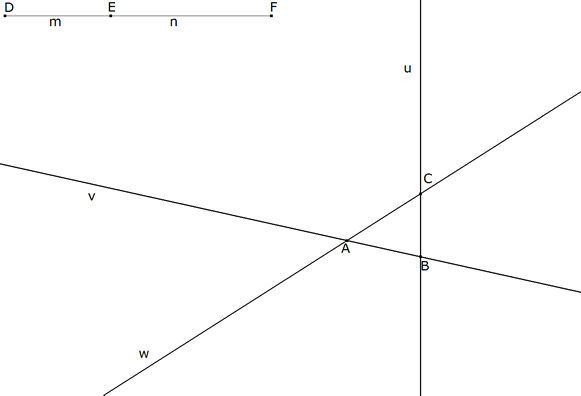figura 70 Dibujamos el enunciado. Las tres rectas dadas u, v, w (forman el triángulo ABC). Los dos segmentos dados DE=m, EF=n (forman el pseudo-triángulo DEF).

3.3.2 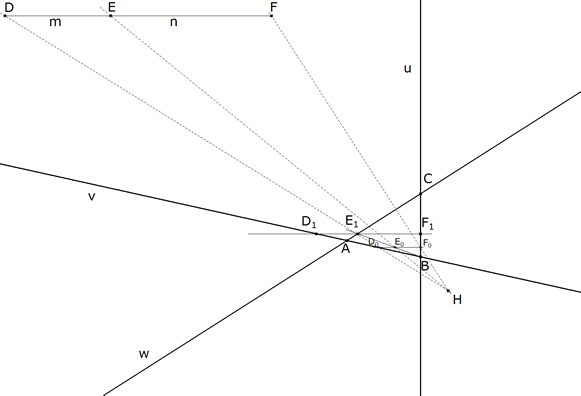figura 71 Según la indicación del enunciado principal: “... se inscribe en el triángulo dado un triángulo de la forma requerida ...” El homólogo de D sobre AB, el homólogo de E sobre CA y el homólogo de F sobre BC. Tomamos sobre AB un punto cualquiera D₀, por D₀ paralela a ED que corta a BC en F_0.. DD₀ y FF₀ se cortan en H centro de homotecia. EH corta a D₀F₀ en E₀. D₀E₀F₀ es homotético a DEF. Para hallar el segmento (triángulo) homotético e inscrito, tomamos B como centro de otra homotecia. La recta BE₀ corta a CA en E₁. Obtenido E₁, por medio de la correspondiente paralela a DEF obtenemos F₁ sobre BC y D₁ sobre AB. D₁E₁F₁ es el segmento (triángulo) homotético (con la forma requerida) inscrito en ABC. A partir de aquí determinaremos otro segmento (triángulo circunscrito) y congruente con DEF.

3.3.3 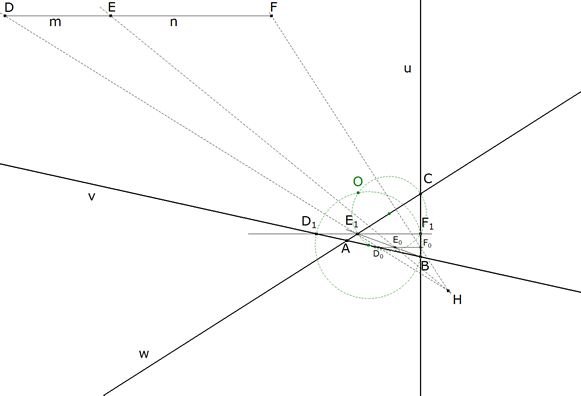figura 72 Según la indicación del enunciado principal: “... y se determina el centro de rotación tratándolo como triángulo fundamental; ...” Supongamos para ello que D₁E₁F₁ son puntos homólogos sobre las tres rectas dadas AB, CA y BC. Si D₁ y E₁ son homólogos, AB y CA se cortan en A; por tanto el centro de rotación está sobre el círculo por D₁, E₁ y A. Si F₁ y D₁ son homólogos, AB y BC se cortan en B; por tanto el centro de rotación está sobre el círculo por F₁, D₁ y B. O está en la intersección de los círculos hallados.

3.3.4 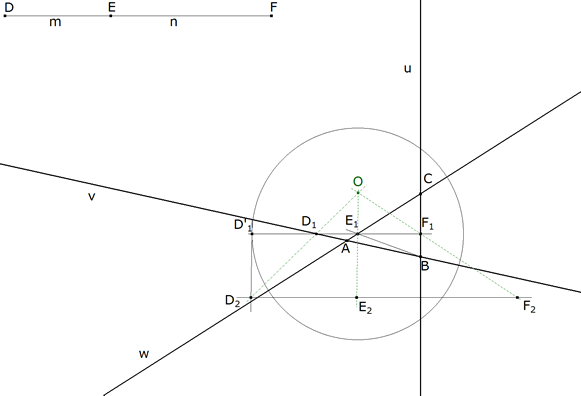figura 73 Hallamos ahora un segmento (triángulo) homotético a D₁E₁F₁ respecto a O y congruente con DEF. Con centro en E₁, círculo de radio ED que corta a E₁D₁ en D’₁. Por D’₁ paralela a OE₁ que corta a OD₁ en el vértice D₂ homólogo de D₁. La paralela a D₁E₁F₁ determina los vértices E₂ y F₂ homólogos a E₁ y a F₁. Tenemos centrado en O a D₂E₂F₂, un segmento (triángulo) idéntico a EDF. Ya sólo nos queda girar este segmento (triángulo) en torno a O hasta que los vértices coincidan con los lados de ABC para obtener la solución.

3.3 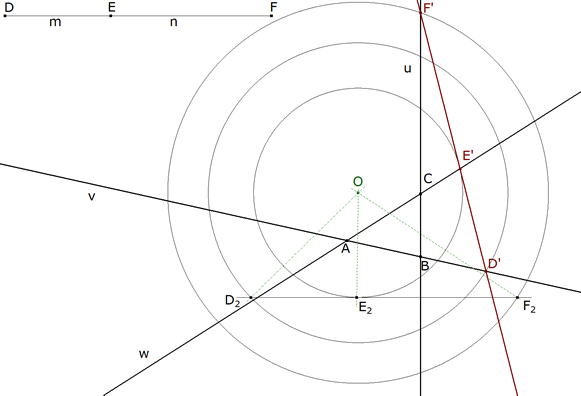figura 74 Para los giros, trazamos tres círculos con centro en O. Para el homólogo de D, el círculo pasa por D₂ homólogo de D₁ y corta a AB por primera vez en D’. Para el homólogo de E, el círculo pasa por E₂ homólogo de E₁ y corta a CA por primera vez en E’. Para el homólogo de F, el círculo pasa por F₂ homólogo de F₁ y corta a BC por primera vez en F’. D’E’F’ es una de las soluciones buscadas.

3.3 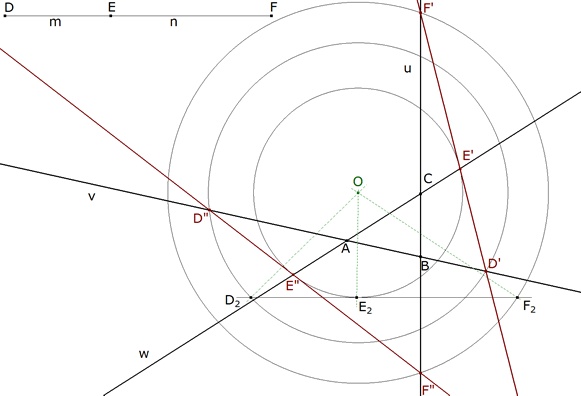figura 75 Como un círculo corta a una recta a lo sumo en dos puntos, la segunda intersección de cada círculo en su lado correspondiente nos proporciona una nueva solución.

3.3.7 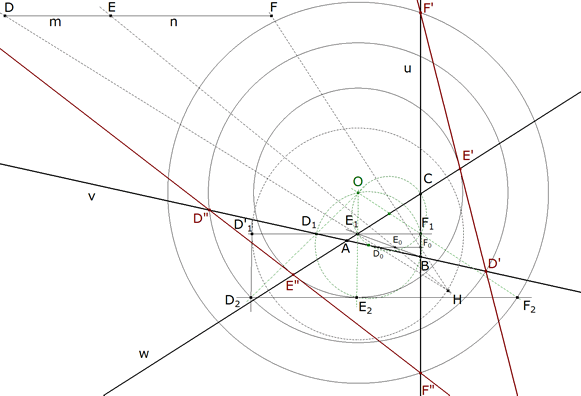figura 76 Así queda la construcción completa con todas sus líneas.