CARACTERIZACIÓN DEL TRIÁNGULO HIO
Vicente Vicario García
“En honor a Leonhard Euler (1707,1783) uno de
los más grandes matemáticos de todos los tiempos, por el tricentenario de su
nacimiento”.
Resumen: En este artículo nuestro objetivo es caracterizar las propiedades más relevantes del triángulo HIO, es decir, el triángulo formado por los puntos notables ortocentro, incentro y circuncentro, respectivamente, de otro triángulo ABC. Inicialmente podemos plantear algunos problemas esenciales en torno a este triángulo: (a) ¿Cómo determinar las longitudes de los lados de un triángulo ABC que tenga como triángulo HIO a uno dado? (b) ¿Qué restricciones debe satisfacer un triángulo HIO dado? (c) ¿Qué condiciones hacen que la solución al problema (a) anterior sea única?,…
HISTORIA DEL PROBLEMA
Como ya hemos indicado, pretendemos hacer modesta memoria de uno de los más eminentes y prolíficos matemáticos de todos los tiempos: Leonhard Euler. Nació en la ciudad suiza de Basilea el 15 de abril de 1707 y su legado matemático es sencillamente imponente [1]. Nos centraremos en una pequeña parte de sus contribuciones a la geometría: La geometría del triángulo. Nadie sostiene que el legado matemático de Euler se base fundamentalmente en sus contribuciones a la geometría, pero es indiscutible que sus resultados en este campo fueron importantes.
Por otra parte, sería erróneo pensar que Euler ignorase o minusvalorase esta materia fascinante, ya que cuatro volúmenes de su Opera Omnia, que totalizan casi 1600 páginas, están dedicadas a la investigación en geometría [2]. Una parte de sus trabajos geométricos se pueden caracterizar bajo el epígrafe de geometría sintética. Sin embargo, la mayoría son relativos a la denominada geometría analítica.
En el año 1765 Euler consideró la determinación de un triángulo ABC a partir del triángulo formado por sus puntos notables H, I, O. Se preguntó sobre las relaciones que debieran ser satisfechas en el triángulo HIO para que un único triángulo ABC tuviese esos puntos notables. En su artículo “Solutio facilis problematum quorundam geometricorum dificillimorum” demostró (aunque la demostración es incompleta)† la existencia del requerido triángulo mediante el tratamiento de las longitudes de los lados del triángulo ABC como ceros de una ecuación cúbica con coeficientes reales. Estos coeficientes eran funciones de las longitudes de los lados del triángulo HIO. Dio la siguiente restricción sobre longitudes de los lados de dicho triángulo para asegurar la existencia de tres raíces reales para dicha ecuación cúbica, raíces que resolvían el problema planteado:
pero desgraciadamente no demostró en qué condiciones estas tres raíces reales de la ecuación cúbica serían positivas, y lo que es más grave, en qué condiciones estas tres soluciones representarían las longitudes de los lados de un triángulo real.
En su artículo, Euler no se interesó aparentemente por las implicaciones geométricas de su solución. Mucho más tarde se demostró que su solución era equivalente a la simple desigualdad
donde G es el baricentro del triángulo, que divide al segmento OH (demostrado por Euler tras un extenso
cálculo en su artículo) en la relación 
. Este bellísimo resultado fue presentado por A. P. Guinand
en 1984 y su significado geométrico es inmediato:
“Sólo los puntos dentro del círculo de diámetro GH y distintos del punto N, punto medio del segmento OH#, son susceptibles de ser el incentro del triángulo ABC que tenga a los anteriores O, G, H como sus puntos notables”.
Este importante círculo es denominado en la literatura “orthocentroidal disc”, por tener como diámetro los puntos H y G. En su artículo, Guinand en contraposición a Euler, consideró los cosenos de los ángulos del triángulo ABC como ceros de una ecuación cúbica con coeficientes reales. Este problema ha recibido un nuevo impulso y consideración por parte de B. Scimeni en 2002 [3], mostrando cómo resolver el problema usando propiedades de la cónica de Kuipert, en 2005 cuando G. C. Smith [4] empleó consideraciones mecánicas y en 2007 por Joseph Stern [5].
DETERMINACIÓN DE LOS LADOS DEL TRIÁNGULO ABC CONOCIDOS LOS LADOS DEL TRIÁNGULO HIO
Utilizaremos la notación habitual en
la geometría del triángulo donde R, r, s,
O, I, H, G, N
representan el radio de la circunferencia circunscrita al triángulo, radio de
la circunferencia inscrita, semiperímetro, circuncentro, incentro, ortocentro,
baricentro, y punto medio del segmento OH
(o centro del círculo de los nueve puntos 
), respectivamente.
Nuestra solución va a considerar los cuadrados de los lados del triángulo ABC como ceros de una ecuación cúbica con coeficientes reales, así que, en este sentido, se parece más a la solución dada por Euler que a la otras demostraciones alternativas ya comentadas.‡
Para analizar en profundidad el
problema deduciremos expresiones para 
, 
e 
en función exclusiva
de R, r y s. Las expresiones a
las que vamos a llegar son clásicas y vienen dadas por
[1]
[2]
[3]
Utilizaremos en la resolución del problema las siguientes relaciones
[4]
[5]
[6]
La relación [4] se puede demostrar fácilmente aplicando el teorema de los senos generalizado al triángulo ABC y relaciones trigonométricas elementales
La relación [5] requiere la
anterior, el teorema de los senos generalizado, la conocida expresión 
para el producto de
los lados de un triángulo, y relaciones trigonométricas elementales
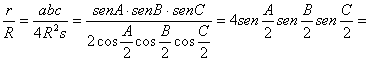
La última podemos obtenerla a partir
del teorema de los cosenos, la fórmula de Herón para el área de un triángulo 
, la relación 
, junto con algunas transformaciones trigonométricas previas
Y entonces, obtenemos las siguientes relaciones
Restando y despejando, obtenemos finalmente la expresión [6] requerida.†
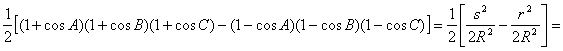
Obtenidas estas expresiones podemos pasar a expresar las longitudes de los lados del triángulo HIO en función de R, r y s. En el caso de OI, es muy conocida la relación de Euler
que se obtiene aplicando el teorema de la potencia al incentro de un triángulo ABC con respecto a la circunferencia circunscrita al mismo.‡
De forma similar determinamos OH . Para ello consideremos el punto A´ donde AH corta de nuevo a la circunferencia circunscrita a ABC. Entonces se tiene que
.
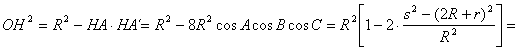
La primera de las igualdades se
encuentra aplicando el teorema de los senos al triángulo AHB, teniendo en cuenta que 
, 
. La
siguiente se obtiene fácilmente aplicando el teorema del ángulo inscrito junto
con sencillas relaciones trigonométricas y observando que 
.
Para determinar IH podemos suponer, sin pérdida de generalidad, que 
. Por otra parte, como 
aplicando el teorema
de los cosenos al triángulo HIA
obtenemos
[7]
Aplicando la relación [5] y teniendo
en cuenta que 
, junto con relaciones trigonométricas del ángulo mitad, tenemos
y también
pero sustituyendo en la expresión anterior [7] entonces
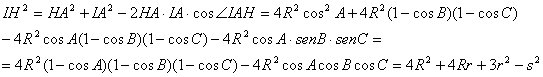
La última igualdad resulta de sustituir las expresiones previas por las ya determinadas en función de R, r y s. Es fácil también verificar la siguiente relación, sin más que utilizar la expresión [5] y el resultado anterior
Nuestro objetivo es ahora expresar R, r y s como funciones exclusivas de OI, OH e IH. Después de manipular algebraicamente las relaciones [1], [2] y [3] ya demostradas, llegamos a
[8]
donde la última
desigualdad se debe a la relación de Euler 
, que surge directamente de la desigualdad 
.† (Observemos que de aquí
también se deduce la desigualdad 
, lo cual restringe valores para la construcción del
triángulo de partida OIH).
Despejando en la relación de Euler
[9]
y también mediante manipulaciones algebraicas tenemos que
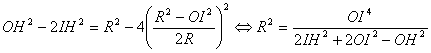[10]
(Observemos
que de esta expresión se deduce que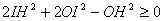 
)
Procediendo de forma análoga
[11]
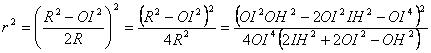[12]
Para
determinar 
despejamos en la
relación [3] anterior y tenemos 
. Sustituyendo las relaciones [9], [10] y [11] en esta
relación y tras manipulación algebraica llegamos a
[13]
Para deducir finalmente relaciones para las longitudes a, b, c de los lados del triángulo ABC en función de las longitudes de los lados de su triángulo OIH, necesitamos expresar las longitudes de los lados del triángulo ABC en función de los valores R, r y s.
Así pues, podemos plantear las relaciones siguientes
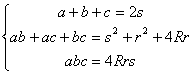[14]
La última de las relaciones anteriores es un resultado clásico y la anterior se puede deducir de
[15]
Para evitar radicales utilizaremos más convenientemente las relaciones
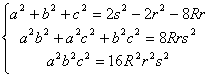[16]
donde estas relaciones se deducen de las relaciones [14] después de observar que
De forma análoga deducimos que
y utilizando las relaciones [14] y el teorema de los senos generalizado
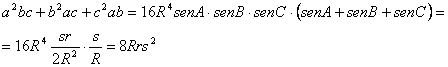
A partir las relaciones de
Cardano-Vieta entre las raíces y coeficientes de una ecuación algebraica
llegamos a que las raíces de la siguiente ecuación cúbica son los cuadrados de
las longitudes de los lados 
del triángulo ABC pedido, siendo los coeficientes de
dicha ecuación determinados de forma racional exclusivamente respecto a los
valores de OI, OH, IH.
[17]
Sustituyendo, y tras manipulación algebraica, podemos expresar la ecuación en la forma
[18]
con los siguientes coeficientes
Para que el problema tenga como solución un triángulo ABC real tenemos que demostrar que la anterior ecuación cúbica admite tres soluciones reales positivas y además susceptibles de formar triángulo. Estas dos condiciones se verifican atendiendo a las siguientes dos proposiciones que fueron, como declara B. Scimeni [3], omitidas en el artículo de Euler ya mencionado y fáciles de demostrar.
Proposición 1: “Tres números reales 
son positivos si y
sólo si 
. 
, 
son todos positivos ”.
Proposición 2: “Tres números reales positivos satisfacen las
desigualdades triangulares 
, 
, 
si y sólo si
”.#
EL TRIÁNGULO HIO ES
OBTUSÁNGULO
A continuación procedemos a demostrar que los segmentos OI, OH, IH además de formar triángulo deben verificar las siguientes relaciones
(a) 
(b) 
(c) 
Las dos primeras relaciones ya han sido deducidas anteriormente (véanse las notas a las relaciones [8] y [10]) y la última se deduce de la relación siguiente
pero esta desigualdad es equivalente a
[19]
La última desigualdad se sigue de 
ya que
Y para la otra desigualdad tenemos
que puesto que 
, entonces se cumple evidentemente que
que a su vez implica
y como
y 
, 
, 
,
entonces
lo que demuestra la desigualdad .
Por otra parte, de nuevo, de la
desigualdad y de la expresión ya
obtenida para IH en función de R, r
y s tenemos la desigualdad
[20]
Aplicando el teorema de los cosenos al triángulo HIO tenemos que
Para demostrar que el triángulo HIO no puede ser acutángulo bastará verificar la desigualdad siguiente
[21]
Además, por la desigualdad
triangular tenemos que 
, 
, 
y aplicando la
desigualdad entre las medias aritmética y geométrica
Ahora bien, por la
fórmula de Herón del área de un triángulo y usando la expresión del área 
tenemos
lo que nos lleva a la desigualdad
[22]
De la conocida
relación triangular 
y, de nuevo,
utilizando la desigualdad entre la medias aritmética y geométrica
[23]
Ahora ya es sencillo demostrar la desigualdad anterior ya que por la desigualdad
pero la última desigualdad es cierta ya que
que es la famosa desigualdad de Euler. La desigualdad dada se torna igualdad si y sólo si el triángulo es equilátero, pero éste no es nuestro caso ya que no tendría sentido tal suposición. Así pues, el triángulo HIO es obtusángulo.
Se puede afinar más y demostrar, con
la notación habitual y siendo, punto medio del segmento OH (centro de la circunferencia de los nueve puntos) la siguiente
relación
[24]
con igualdad si y
sólo si 
.
Para ello denotaremos las longitudes
de los segmentos OI, IH, OH
por x, y, z respectivamente
y 
. Podemos entonces reescribir las longitudes
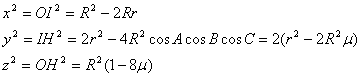[25]
Designaremos 
. Aplicando entonces el teorema de los cosenos y las
expresiones anteriores tenemos
. [26]
Esto demuestra de
nuevo que
y el ángulo 
es obtuso. Además,
puesto que 
, podemos escribir
Pero
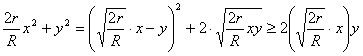
con igualdad si y
sólo si 
. Por tanto, se deduce fácilmente que
[27]
con igualdad si y sólo si, por la relación anterior
En el triángulo HIO la mediana que parte del vértice I es IN. Si denotamos 
y aplicamos el teorema
de Stewart, llegamos fácilmente a la relación
[28]
Pero , (por el teorema de Pitágoras y su recíproco) si y sólo si
se cumple la relación 
, que ocurre, por la relación anterior si y sólo si
Resultados análogos son válidos para
los otros ángulos del triángulo HIO.
Mencionamos, por ejemplo, que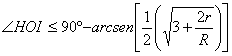 
, con igualdad si y sólo si 
, o de forma equivalente, 
.
EL TRIÁNGULO HIO
PUEDE SER ISÓSCELES
Podemos preguntarnos si el triángulo
HIO puede ser isósceles y qué
condiciones debe de cumplir el triángulo ABC
para originar tal triángulo. Sabemos por las desigualdades ya estudiadas que
ni OI,
ni IH
pueden ser de longitud mayor que la del segmento OH, así que el único modo de que el triángulo HIO sea isósceles es que . Ahora, como y . Entonces si y sólo si 
. Reordenando términos tenemos que la igualdad anterior es
equivalente a la siguiente
[29]
Por otra parte es bien conocido que . Además, de la identidad
y observando que 
y que
se tiene, después de simplificar que
así que la relación es equivalente a
[30]
Otra
condición equivalente a apareció en el
problema E2282 (1971,196; 1972,397) de American Mathematical Monthly, y es que
el triángulo ABC tenga un ángulo
igual a 60º.
APÉNDICE
Deduciremos una serie de expresiones relacionadas con los cosenos de los ángulos de un triángulo. Demostraremos la siguiente proposición:
Proposición: “Con la notación habitual para un triángulo sea A un ángulo del mismo, entonces cosA es una raíz real de la ecuación polinómica siguiente:
”.
Para
la demostración consideremos las relaciones 
(teorema de los senos
generalizado) y 
(relacionada con el incentro). Utilizando las identidades
trigonométricas del ángulo doble
Elevando al cuadrado y operando
se tiene
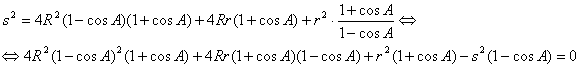
de donde, después de manipulaciones algebraicas, llegamos a la relación que queremos
.
Claramente, esta relación se cumple también para 
y 
. De las relaciones de Cardano-Vieta entre las raíces y los
coeficientes de una ecuación algebraica, deducimos las siguientes relaciones:
[1]
La última de las identidades anteriores es la relación [6] demostrada por otros métodos a lo largo del artículo. Esta proposición es más general que los resultados aislados ya obtenidos por métodos elementales. Con este método de demostración podemos obtener fácilmente dos corolarios interesantes:
Corolario1: “Si A es el mayor de los ángulos del
triángulo ABC, entonces:
Si
Si
Si
”
Para la demostración basta observar la última de las expresiones [1] de este apéndice
Corolario 2: “Si A, B, C son los ángulos de un triángulo
acutángulo entonces 
”
Para
la demostración basta aplicar el corolario anterior y la desigualdad de Euler teniendo que 
.
REFERENCIAS
[1] C. B. Boyer, Historia de la Matemática. Alianza Universidad Textos. 1986
[2] W. Dunham, EULER, el maestro de todos los matemáticos. Ed. Nivola,2000
[3] B.
Scimeni, Paper-Folding and Euler´s Theorem Revisited. Forum Geometricorum, FG
(2002).
[4]
G. C. Smith, Statics and the Moduli Space of Triangles. FG (2005)
[5]
J. Stern, Euler´s Triangle Determination Problem. FG (2007)
[6] V. Vicario, Solución al problema 134 de la revista OIM.
---oooOooo---
aparece bajo el símbolo de raíz cuadrada en la expresión para
el área de un triángulo de la fórmula de Herón.