Problema 429
Bernat, P, y Morinet-Lambert, J. (1996): A new way for visual reasoning in geometry education. Springer Berlin / Heidelberg (p. 452)
Ejercicio: Sea ABC un triángulo. C’ y B’ sean los puntos medios de los lados AB y AC. J es el simétrico de C según C`. I es el simétrico de B según B’. Demostrar que A es el
punto medio de IJ.
Solución.
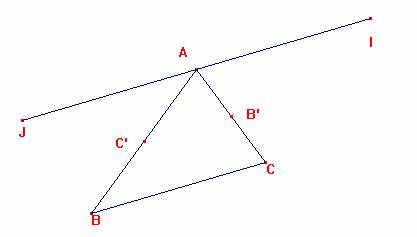
El segmento AI es el transformado de C’B’ en una homtecia de razón 2 y centro B.
El segmento AJ es el transformado de B’C’ en una homotecia de razón 2 y centro C.
Luego AI = 2C’B’, y JA=2C’B’. Luego ambos AI y AJ son paralelos a C’B’ y miden igual. Así A es punto medio de JI. Cqd.
Ricardo Barroso Campos.
Didáctica de las Matemáticas
Universidad de Sevilla