Problema 430

Consideremos, por ejemplo, el llamado “Teorema de Napoleón”, a menudo atribuido a Napoleón Bonaparte (que fue un buen joven estudiante de matemáticas). Sean tres triángulos equiláteros construidos hacia fuera de cualquier triángulo. Los centros de los equiláteros forman también un triángulo equilátero. Uno puede imaginar al joven Napoleón con papel, regla, y compás, comenzando con un triángulo cualquiera, descubriéndolo de manera experimental. Este descubrimiento era así suficiente para asegurar la certeza del teorema general, con una alta probabilidad.

Davis, P.J. (1977)Proof, Completeness, Transcendentals, and Sampling.Journal. of the Association for Computing Machinery 24, 298-310. April. (p. 307)

Solución tomada de

cut-the-knot

Por Dr. Scott Brodie, Dr.
Mount Sinai School of Medicine, NY

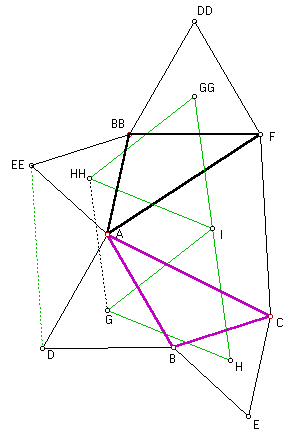
Sea ABC el triángulo original. Sean D, E y F en el exterior tal que ADB, BEC y AFC sean equiláteros, cuyos baricentros sean G, H e I. Demostremos que <HIG=60º. Tomemos I como centro de giro, y rotemos la figura entera 120º, superponiéndose sobre la figura original. Según el giro, A->F, F->C y C->A, I->I, B->BB, D->DD, E->EE, G->GG, y H->HH, respectivamente. Unamos D a EE y G a HH. Por la rigidez del giro, ΔG H I = Δ GG HH I. En particular, G H = GG HH. Consideremos ahora los seis triángulos que comparten el vértice A. Tres de ellos son equiláteros (ABD, ACF, y A EE BB).

<BB A F=<BCA, <D A EE =<ABC y el pentágono A BB EE D B es congruente con el pentágono BECAD. Por ello, G HH = GH, y G HH = GH = GG HH.

Repitiendo el giro 120º y uniendo otros equiláteros, se obtiene la figura de la derecha. Arguyendo como anteriormente, el hexágono central es equilátero, y los seis triángulos que están alrededor del centro de rotación son congruentes. Entonces, 6 * <HIG=360º, y <HIG=60º. Dado que el centro de rotación I ha sido arbitrario, HIG es equiangular, y por tanto, equilátero, cqd.