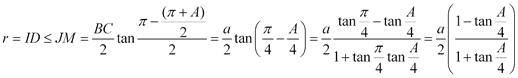Problema 401 .

Construir un triángulo dado : Un lado a, el inradio r, y la medida del ángulo A opuesto al lado a.

Hiebert, J (1986): Conceptual and procedural knowledge: The case of mathematics. Lawrence Erlbaum Associates, Publishers. London. (p. 245)

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de mayo de 2008)

Solución

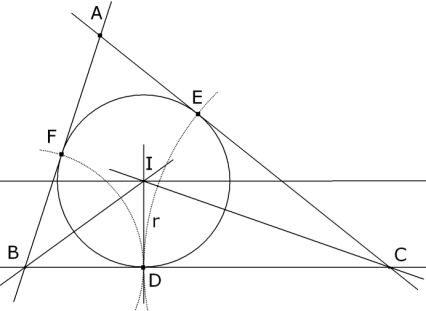
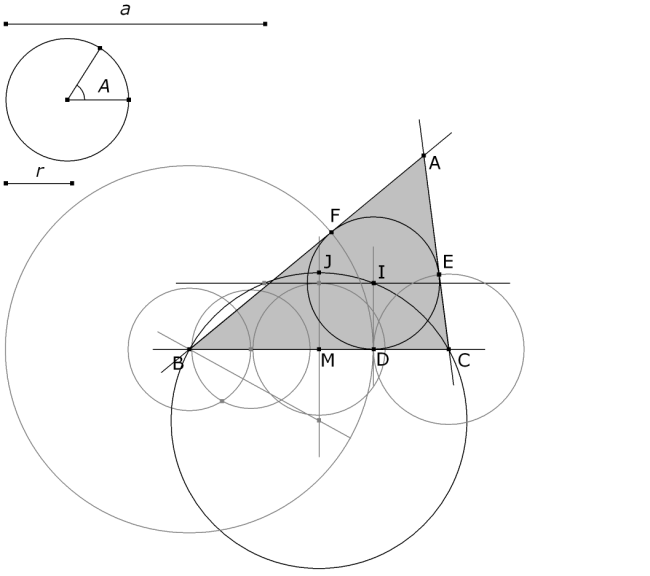
Supongamos el problema resuelto y estudiemos la figura.

Sabemos que BC = a y conocemos el ángulo BAC.

Como el centro del círculo inscrito I está sobre las bisectrices se cumple que el ángulo IBC es ½ B y el ángulo ICD es ½ C.

En el triángulo IBC se cumple la suma de ángulos π = IBC + ICB + BIC y por tanto el ángulo BIC es

π - ½ B - ½ C = π - ½ (B + C) = π - ½ (π - A) = ½ (π + A)

Como conocemos r, podemos establecer que I está en el arco capaz del ángulo ½ (π+A) y cuerda BC y en una paralela a distancia r de BC.

Si D es el punto de contacto del círculo inscrito con el lado BC y E, F los puntos de contacto con los otros lados, entonces tenemos que CE = CD y BF = BD.

• Por una recta cualquiera que pasa por un punto B del plano, trazamos un punto C tal que BC = a.


• Trazamos el arco capaz de ángulo ½ (π + A) en el segmento BC.


• Trazamos una paralela a distancia r de BC que corta al arco anterior en I el incentro del triángulo buscado.


• Trazamos por I una perpendicular a BC cuyo pie es el punto de contacto D.


• Trazamos el círculo inscrito de centro I y radio ID.


• El círculo de centro C y radio CD corta al círculo inscrito en el punto de contacto E.


• El círculo de centro B y radio BD corta al círculo inscrito en el punto de contacto F.


• Las rectas CE y BF son los lados del triángulo concurrentes en A.


• ABC es el triángulo buscado.

que puede escribirse como