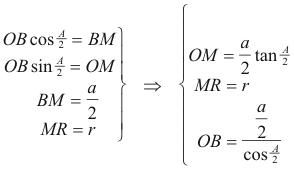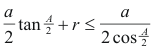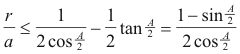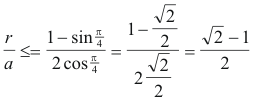Problema 401 (Para el aula ) Construir un triángulo dado : Un lado a, el inradio r, y la medida del ángulo A opuesto al lado a. Hiebert, J (1986): Conceptual and procedural knowledge: The case of mathematics. Lawrence Erlbaum Associates, Publishers. London. (p. 245) Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (2 de septiembre de 2007) |
|
ANÁLISIS DEL PROBLEMA |
|
Supongamos en primer lugar que tenemos el problema resuelto.
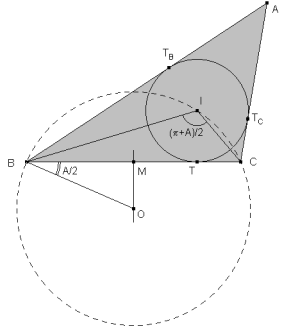
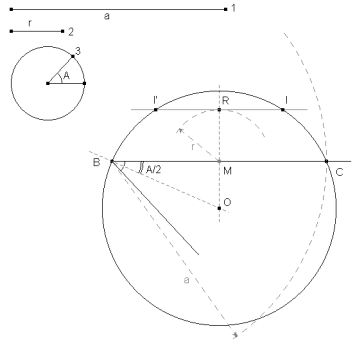
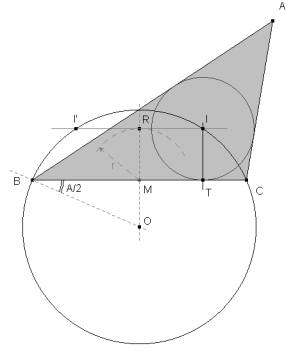
figura 1 El incentro I, estará sobre uno de los arcos capaces del segmento BC; el ángulo de dicho arco es ∡BIC. En el triángulo BIC y teniendo en cuenta que I está en la intersección de las bisectrices de los ángulos B y C
Si consideramos el arco opuesto el ángulo sería el suplementario
Para hallar el centro O del círculo que contiene a los arcos anteriores, trazaríamos, por B, una recta que formara este último ángulo con la recta BC y luego el centro estaría en la perpendicular por B a esta última recta; pero esa perpendicular formará con BC un ángulo complementario al anterior
Por tanto el centro O está sobre una recta por B que forme con BC un ángulo igual a A/2. Además O está también en la mediatriz del segmento BC. Obtenemos O como intersección de los dos lugares anteriores. El círculo de centro O que pasa por B y C es el lugar geométrico del incentro I. En el enunciado del problema, se dice que el radio del círculo inscrito es r; por tanto, I está a una distancia r del lado BC. La paralela a BC, distante de BC la distancia r, es el lugar geométrico del incentro I. Por tanto el incentro I es el punto de intersección de los dos lugares anteriores. Una perpendicular por I a BC nos determina el punto de contacto T del círculo inscrito con el lado BC. Queda determinado el círculo inscrito como el círculo de centro I y radio IT=r. Las tangentes desde B y C al círculo inscrito son respectivamente los lados BA y CA del triángulo buscado. Dichas tangentes determinan a su vez el vértice A. |
|
SOLUCIÓN |
|
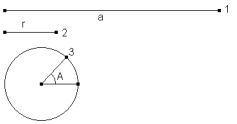
figura 2 Introducimos los datos del enunciado; un segmento variable de longitud a, un segmento variable de longitud r y un ángulo variable A. 1, 2, 3 serán los puntos variables en una construcción dinámica.
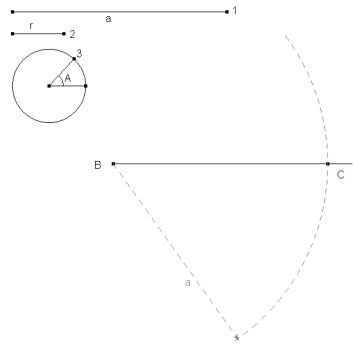
figura 3 Por un punto B (variable en una construcción dinámica) del plano trazamos una recta cualquiera. Y con centro en B trazamos un arco de radio a que corta a la recta anterior en C
figura 4
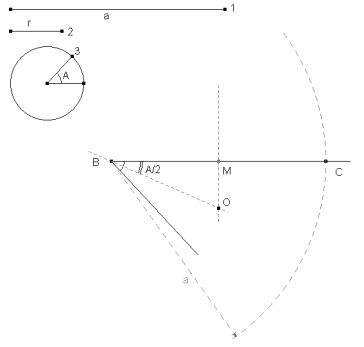
Trazamos por B una recta que forme el ángulo dado A con la recta BC. Su bisectriz formará un ángulo igual a A/2. Trazamos la mediatriz de BC que en su intersección con la bisectriz anterior nos da el punto O.
figura 5 Con centro en O trazamos el círculo por B y C que es el primer lugar del incentro. Con centro en M, punto medio de BC, trazamos un arco de radio r que corta OM en R. La paralela a BC por R nos da el segundo lugar geométrico del incentro. La intersección de los dos lugares nos da el punto I (la otra intersección I’ nos daría una segunda solución simétrica a la primera respecto a OM).
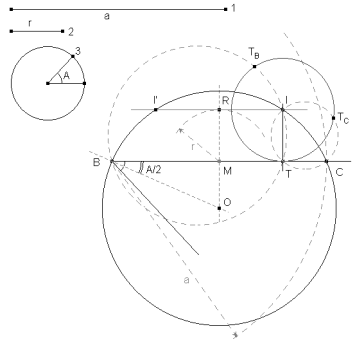
figura 6 Una perpendicular desde I encuentra a BC en T. El círculo por T con centro en I es el círculo inscrito del triángulo buscado. El círculo de diámetro BI corta al círculo inscrito en los punto de contacto de las tangentes desde B. Obtenemos TB. El círculo de diámetro CI corta al círculo inscrito en los punto de contacto de las tangentes desde C. Obtenemos TC.
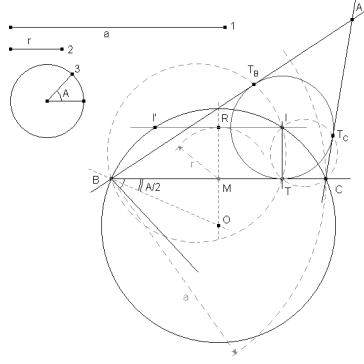
figura 7 Las rectas BTB y CTC se encuentran en el vértice A.
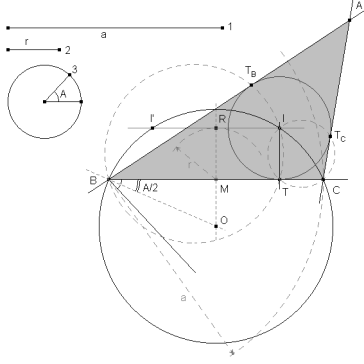
figura 8 ABC es el triángulo buscado. |
|
CONSTRUCCIÓN DINÁMICA |
|
(necesita el plug-in de CABRI II Plus)
PUEDE MOVER LOS PUNTOS 1, 2, 3 y B |
|
DISCUSIÓN |
|
figura 9 Observando la figura vemos que la condición para que exista la construcción es
pero
de donde la condición se escribe
y de aquí
Por ejemplo, si el triángulo fuera rectángulo en A
|