|
Para el aula. Problema 402. TRIÁNGULOS PITAGÓRICOS Prácticamente todo el mundo conoce que 32 + 42 = 52 es la más simple aplicación del Teorema de Pitágoras que establece que la suma de los cuadrados de los catetos de un triángulo rectángulo es igual al cuadrado de la hipotenusa. Pero en comparación muy pocos conocen que 5, 12, y 13 satisfacen la misma relación sin ser proporcionales a 3, 4 y 5. Y muchos menos todavía podrían dar los lados de un tercer “triángulo pitagórico” distinto de los dos mencionados, por ejemplo, 7, 24 y 25. Recreations in the theory of numbers (The queen of mathematics entertains). Albert H. Beiler. Dover Publications Inc. Los triángulos rectángulos con lados enteros reciben el nombre de triángulos pitagóricos.
Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (15 de septiembre de 2007) |
|
| APARTADO (A) |
|
|
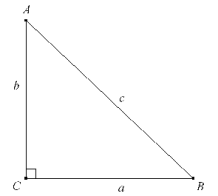
Dibujamos ahora el enunciado.
TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que, en un triángulo rectángulo, el cuadrado construido sobre la hipotenusa es igual a la suma de los cuadrados sobre los dos catetos. Si c es la longitud de la hipotenusa y a, b las longitudes de los dos catetos, el teorema se expresa como
LA RESTRICCIÓN A LOS NÚMEROS ENTEROS NO ES IMPRESCINDIBLE Si encontramos cualquier solución racional para Eq.[1], podemos escribir los tres números con un denominador común
de lo que se deduce
que es una solución entera. LA SOLUCIÓN PRIMITIVA Sólo precisamos hallar las soluciones enteras primitivas de la ecuación Eq.[1]; es decir, las soluciones en las que no hay un factor común para a, b y c, porque si tal factor d existe, lo eliminamos dividiendo todos los componentes de la ecuación entre d2. Para una solución primitiva los números de cualquier par formado con a, b, c, deben ser primos entre sí. Supongamos, por ejemplo, que a y b tienen un factor común d; el lado izquierdo de Eq.[1] y de ahí también c2 serían divisibles entre d2; pero en ese caso c sería divisible entre d, en contra de la hipótesis de que la solución es primitiva. EN UNA SOLUCIÓN PRIMITIVA a Y b NO PUEDEN SER AMBOS PARES O AMBOS IMPARES Para ello, vemos primero que el cuadrado de un número impar da resto 1 al dividirlo entre 4
y que el resto de dividir entre 4 el cuadrado de un número par es 0
Si suponemos que a y b son simultáneamente pares y trasladamos Eq.[4] y Eq.[5] a Eq.[1], obtenemos
y, en consecuencia, c2 ha de ser múltiplo de 4 y c ha de ser par y por tanto los tres números han de tener un factor común en contra de la hipótesis de que la solución es primitiva. Si suponemos que a y b son simultáneamente impares y trasladamos Eq.[4] y Eq.[5] a Eq.[1], obtenemos
y, en consecuencia, c2 ha de tener resto 2 al dividirlo entre 4, en lugar de 0 según los resultados anteriores. SUPONEMOS QUE a ES EL CATETO PAR Siguiendo con el párrafo anterior, si a es par, b debe ser impar, trasladando Eq.[4] y Eq.[5] a Eq.[1]
y c, en consecuencia, también es impar y no tiene factores comunes con b. Eq.[1] puede escribirse como
De acuerdo con lo precedente, ambos lados de Eq.[9] son divisibles entre 4
por lo que podemos escribir
donde los dos factores enteros de la derecha de Eq.[11] son primos entre sí, ya que cualquier factor común d dividiría simultáneamente a la suma y a la diferencia de los mismos. Pero como
y b, c son primos entre sí, entonces d = 1. Cuando dos factores son primos entre sí, sus factores primos son distintos y su producto no puede ser un cuadrado salvo que sea un cuadrado cada uno de los factores. En consecuencia, podemos escribir
y de aquí, sustituyendo en Eq.[12]
SI s ES PAR, t DEBE SER IMPAR Y VICEVERSA Para asegurar que esta solución es realmente primitiva, observamos que cualquier factor común de b y c ha de dividir a la suma y a la diferencia de estos números. Pero ya que
y ya que s y t son primos entre sí, por serlo sus cuadrados (Eq.[11]), el único factor común posible es 2. Excluiremos este factor tomando uno de los números (s y t) par y el otro impar. LA SOLUCIÓN ENTERA MÁS GENERAL A partir de la solución primitiva más general de Eq.[14], donde s y t son enteros sujetos a las condiciones establecidas, podemos encontrar la solución general en enteros para la ecuación Eq.[1] multiplicando por un entero arbitrario k.
UNA CURIOSIDAD FINAL ¿Cuándo la hipotenusa difiere de uno de los catetos en una unidad?
Este primer caso no puede ser ya que nos conduce a la ecuación Eq.[18] sin solución en Z
La otra posibilidad
que sustituido en Eq.[14] nos proporciona
|
|
| APARTADO (B) |
|
|
En este apartado, trabajamos, cuando se precisa, en el cuerpo Z/(3) y en el cuerpo Z/(5). SI a NO ES DIVISIBLE ENTRE 3 Si a sí es divisible entre 3, ya tenemos un lado del triángulo que cumple la primera condición del apartado (B). Si no es así, veamos que significa esta condición
En principio, parece que hay que estudiar 4 casos; pero la simetría de las ecuaciones Eq.[14] nos indica que las soluciones halladas para a, b y c son en valor absoluto las mismas variando alguno de sus signos y por eso sólo hace falta comprobar los casos en los que varían los valores positivos de los parámetros a considerar. Aquí, los 4 casos se reducen a 1
que introducido en Eq.[14] nos lleva a
que nos indica que si a no es divisible entre 3, ¡siempre! lo es b. SI b NO ES DIVISIBLE ENTRE 3 Si b sí es divisible entre 3, ya tenemos un lado del triángulo que cumple la primera condición del apartado (B). Si no es así, veamos que significa esta condición
haciendo el siguiente cambio
y aplicándolo a Eq.[24], obtenemos
Por un razonamiento análogo al del caso anterior, sólo hace falta considerar el caso
que nos lleva a
que nos indica que si b no es divisible entre 3, ¡siempre! lo es a. Por lo tanto, EN UN TRIÁNGULO PITAGÓRICO UNO DE LOS DOS CATETOS ES DIVISIBLE ENTRE 3; NUNCA LA HIPOTENUSA SI a NO ES DIVISIBLE ENTRE 5 Si a sí es divisible entre 5, ya tenemos un lado del triángulo que cumple la segunda condición del apartado (B). Si no es así, veamos que significa esta condición
En principio, parece que hay que estudiar 16 casos; pero la simetría de las ecuaciones Eq.[14] nos indica que las soluciones halladas para a, b y c son en valor absoluto las mismas variando alguno de sus signos y por eso sólo hace falta comprobar los casos en los que varían los valores positivos de los parámetros a considerar. Aquí, los 16 casos se reducen a 3
que introducidos en Eq.[14] nos llevan a
que nos indica que si a no es divisible entre 5, ¡siempre! lo es b o lo es c SI b NO ES DIVISIBLE ENTRE 5 Si b sí es divisible entre 5, ya tenemos un lado del triángulo que cumple la segunda condición del apartado (B). Si no es así, veamos que significa esta condición
y aplicando Eq.[25] a Eq.[32]
Sólo hace falta considerar 3 casos
donde hemos usado -3=2 (mod.5) porque simplifica mejor; eso nos lleva a
que nos indica que si b no es divisible entre 5, ¡siempre! lo es a o lo es c Por lo tanto, EN UN TRIÁNGULO PITAGÓRICO, UNO DE LOS DOS CATETOS O LA HIPOTENUSA ES DIVISIBLE ENTRE 5 a ES SIEMPRE DIVISIBLE ENTRE 4 Si recordamos que s y t han de ser de paridades distintas, podemos poner
Como a es siempre divisible entre 4 y uno de los catetos es siempre divisible entre 3 tendremos
Por lo tanto, EN UN TRIÁNGULO PITAGÓRICO, EL PRODUCTO DE LOS DOS CATETOS ES SIEMPRE DIVISIBLE ENTRE 12 y como hemos visto que uno de los catetos o la hipotenusa es siempre divisible entre 5, tenemos
Por lo tanto, EN UN TRIÁNGULO PITAGÓRICO, EL PRODUCTO DE LOS TRES LADOS ES SIEMPRE DIVISIBLE ENTRE 60 |
|
| APARTADO (C) |
|
|
LA EXPRESIÓN DE LAS DISTINTAS BISECTRICES EN FUNCIÓN DE LOS LADOS EN UN TRIÁNGULO PITAGÓRICO Si tenemos en cuenta Eq.[14], podemos expresar el semiperímetro del triángulo como
y como las bisectrices de los ángulos agudos son
la expresión de estas bisectrices en función de Eq.[14] nos queda como
SI EL ÁNGULO AGUDO CONSIDERADO ES A, EL OPUESTO A a EL CATETO PAR Vistas las fórmulas anteriores, vemos que las bisectrices (interior y exterior) del ángulo A son simultáneamente RACIONALES si
es decir, si la suma de dos cuadrados es un cuadrado. Este problema ya lo hemos resuelto al principio y aprovechando, de nuevo, Eq.[14], podemos escribir
Visto lo cual, podemos enunciar que EN UN TRIÁNGULO PITAGÓRICO, LA BISECTRIZ DEL ÁNGULO AGUDO OPUESTO AL CATETO PAR SÍ PUEDE SER RACIONAL SI EL ÁNGULO AGUDO CONSIDERADO ES B, EL OPUESTO A b EL CATETO IMPAR Vistas las fórmulas anteriores vemos que las bisectrices (interior y exterior) del ángulo B son simultáneamente RACIONALES si
pero si un cuadrado entero es divisible entre 2, es par y por tanto divisible entre 4
ecuación que nos indica que la suma de cuadrados de s y t es par; pero sabemos que s y t son de distinta paridad y por lo tanto la suma de sus cuadrados debe ser impar, lo que nos conduce a una contradicción que nos lleva enunciar que EN UN TRIÁNGULO PITAGÓRICO, LA BISECTRIZ DEL ÁNGULO AGUDO OPUESTO AL CATETO IMPAR NO PUEDE SER RACIONAL |
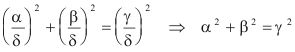 Eq.[3]
Eq.[3]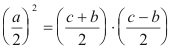 Eq.[11]
Eq.[11]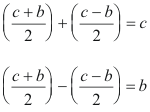 Eq.[12]
Eq.[12]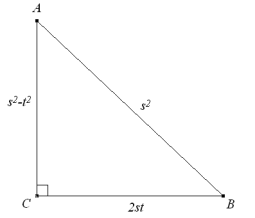
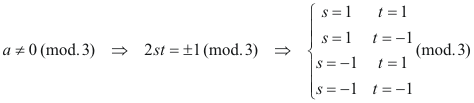 Eq.[21]
Eq.[21]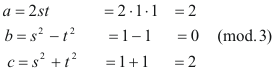 Eq.[23]
Eq.[23]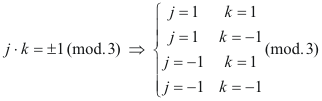 Eq.[26]
Eq.[26]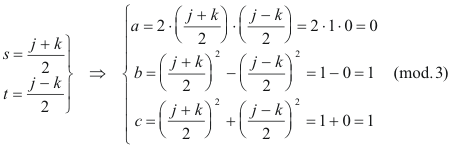 Eq.[28]
Eq.[28]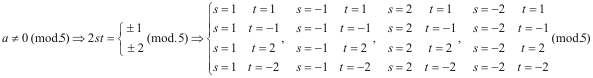 Eq.[29]
Eq.[29]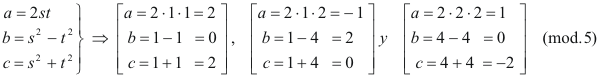 Eq.[31]
Eq.[31]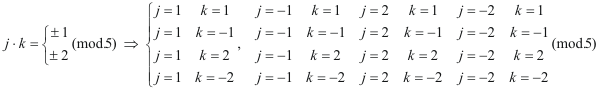 Eq.[33]
Eq.[33]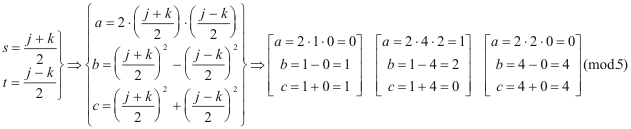 Eq.[35]
Eq.[35]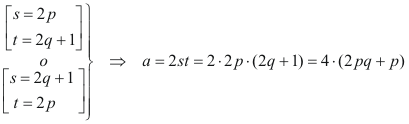 Eq.[36]
Eq.[36]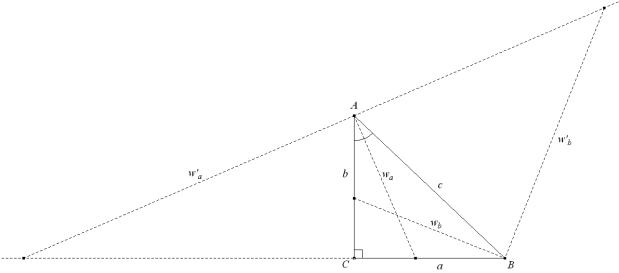
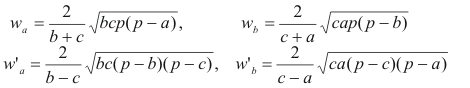 Eq.[40]
Eq.[40]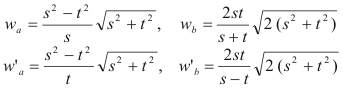 Eq.[41]
Eq.[41]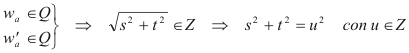 Eq.[42]
Eq.[42]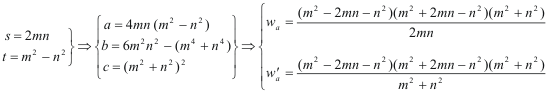 Eq.[43]
Eq.[43]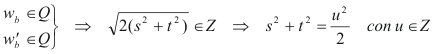 Eq.[44]
Eq.[44]