Problema 402. Prácticamente todo el mundo conoce que es la más simple aplicación del teorema de Pitágoras. Pero en comparación muy pocos conocen que satisfacen la misma relación sin ser proporcionales a 3, 4 y 5. Y mucho menos, por ejemplo, .

Los triángulos rectángulos de lados enteros reciben el nombre de triángulos pitagóricos.

(a) Hallar las fórmulas que dan los lados enteros para un triángulo rectángulo

(b) Mostrar que en todo triángulo pitagórico: Hay uno de los lados que es siempre divisible por 3 y uno por 5. El producto de los catetos es divisible por 12 y el producto de los tres lados es divisible por 60

(c) Hallar, como propone (Diofanto de Alejandría en el problema 18 del libro VI de su Aritmética) los triángulos pitagóricos en los que la longitud de la bisectriz de uno de los ángulos agudos es racional

Resolución: (Vicente Vicario García, Huelva)

(a) Para mayor comodidad emplearemos el lenguaje de las congruencias. Deduciremos la solución general en números enteros de la ecuación x² + y² = z². Las soluciones (x, y, z) se denominan ternas pitagóricas. Basta determinar tales ternas con (x, y, z) primos entre sí (dos a dos) y con y par porque si x e y fueran ambos impares, tendríamos z² ≡ 2 que es imposible.

Escribiendo la ecuación en la forma (z + x)(z – x) = y² y observando que obviamente , obtenemos que z + x = 2u², z – x = 2v² e y = 2uv para u, v enteros positivos primos entre sí. Esto da: x = u² – v², y = 2uv, z = u² + v². Además, puesto que z es impar, vemos que u y v tienen paridad opuesta. Recíprocamente, se verifica fácilmente que si u, v son enteros positivos primos entre sí y de paridad opuesta, entonces, los x, y, z anteriores proporcionan una terna pitagórica con x, y, z primos entre sí e y par. De este modo, la solución general de la ecuación es: x = k(u² – v²), y = k2uv, z = k(u² + v²) con u, v números naturales primos entre sí y de paridad opuesta y k un número natural arbitrario no nulo.

(b) Para demostrar que uno de los lados es siempre múltiplo de 3 observemos que si ninguno de los es múltiplo de 3, entonces para cada uno de ellos se tendría que , , , lo que es absurdo, ya que tendríamos .

Para demostrar ahora que siempre uno de ellos es divisible por 5 procederíamos de forma análoga, observando que si ninguno de los es múltiplo de 5, se tendría ahora que , , , lo que sería absurdo, ya que

Por otra parte el producto de los catetos es siempre múltiplo de 12 ya que lo es por 4 puesto que u y v tienen paridad opuesta y, por tanto, uno de ellos es par y además, si ni u, ni v son múltiplos de 3, entonces, al menos uno de los factores o bien ha de ser divisible por 3. Finalmente, el producto de los tres lados es divisible por 60 ya que lo es por 12 y por 5.

(c) Analizaremos primero el caso relativo a la bisectriz interior de uno de los ángulos agudos. Utilizaremos una de las expresiones clásicas que nos da la longitud de la bisectriz interior que parte del vértice A en un triángulo arbitrario ABC

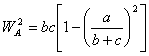
Suponiendo ahora que el triángulo es rectángulo y de lados enteros, al sustituir los valores de los lados determinados anteriormente (ternas pitagóricas) obtenemos

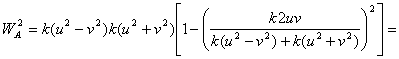
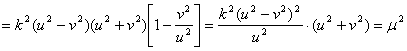con

Evidentemente el primer factor del producto de la última igualdad anterior siempre es el cuadrado perfecto de un número racional. Para que sea racional bastaría con que sea también el cuadrado perfecto de un número racional. Por tanto, en este caso, basta elegir , con e y f números naturales primos entre sí y de paridad opuesta. En particular, podemos conseguir triángulos pitagóricos donde la bisectriz interior de uno de los ángulos agudos no sólo sea racional, sino entera. Por ejemplo, escogiendo , obtenemos el triángulo pitagórico en el que la bisectriz interior del mayor de los ángulos agudos es .