Problema 403

Demostreu que si una recta divideix un triangle en dos polígons del mateix perímetre i la mateixa àrea, aleshores ha de passar per l’incentre I de . Demostreu també, sense necessitat de construcció geomètrica, l’existència de tal recta.

Solució de Ricard Peiró:

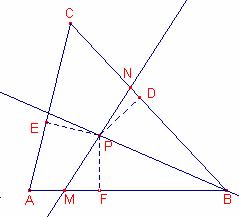Suposem que la recta r talla el costat en el punt M i el costat en el punt N, de manera que el triangle i el quadritàter AMNC tinguen el mateix perímetre i la mateixa àrea.

Per tindre el mateix perímetre:

(1)

Siga P el punt intersecció de la recta r i la bisectriu a l’angle B.

Siguen D, E, F les projeccions de P sobre els costats , i , respectivament.

Aleshores, per P pertànyer a la bisectriu, .

Vegem que P és l’incentre.

.

.

Per hipòtesi, , aleshores:

(2)

Multiplicant l’expressió (1) per :

(3)

Restant les expressions (2) (3):

Aleshores,

El punt P equidista dels costats del triangle, aleshores P és l’incentre.

Demostrem que existeix una recta que passa per l’incentre del triangle i divideix el triangle en dos polígons que tenen la mateixa àrea i el mateix perímetre. Provem que si una recta t que passa per l’incentre i divideix el triangle en dos polígons del mateix perímetre aleshores, els polígons també tenen la mateixa àrea, i viceversa:

Siga P l’incentre del triangle.

.

El perímetre del triangle és igual al perímetre del quadritàter AMNC.

Aleshores sempre hi ha una recta que bisecta l’àrea del triangle i passa per l’incentre, aquesta recta també dividirà el triangle en dos polígons d’igual perímetre.