Problema 403

Demostrar que si una recta divide a un triángulo ABC en dos polígonos del mismo perímetro y de la misma área, entonces debe pasar por el incentro I de ABC. Demostrar también, sin necesidad de construcción geométrica, la existencia de tal recta.

[Este problema es una nueva visión del problema 138 de la quincena del 1 al 15 de febrero de 2004, con una profundización]

Vicario, V. (2007): Comunicación personal.

Solución de Ricard Peiró:

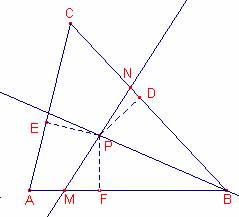Supongamos que la recta r corta el lado en el punto M y el lado en el punto N, de manera que el triángulo y el cuadrilátero AMNC tengan el mismo perímetro y la misma área.

Por tener el mismo perímetro:

(1)

Sea P el punto intersección de la recta r y la bisectriz del ángulo B.

Sean D, E, F las proyecciones de P sobre los lados , y, respectivamente.

Entonces, por P pertenecer a la bisectriz, .

Veamos que P es el incentro.

.

.

Por hipótesis, , entonces:

(2)

Multiplicando la expresión (1) por :

(3)

Restando las expresiones (2) (3):

Entonces,

El punto P equidista de los lados del triángulo, entonces P es el incentro.

Demostremos que existe una recta que pasa por el incentro del triángulo y divide el triángulo en dos polígonos que tienen la misma área y el mismo perímetro. Probemos que si una recta t que pasa por el incentro y divide el triángulo en dos polígonos del mismo perímetro entonces, los polígonos también tienen la misma área, y viceversa:

Sea P el incentro del triángulo.

.

El perímetro del triángulo es igual al perímetro del cuadrilátero AMNC.

Entonces siempre hay una recta que bisecta el área del triángulo y pasa por el incentro, esta recta también dividirá el triángulo en dos polígonos de igual perímetro.