Problema 403 - Demostrar que si una recta divide a un triángulo ABC en dos polígonos del mismo perímetro y de la misma área, entonces debe pasar por el incentro I de ABC. Demostrar también, sin necesidad de construcción geométrica, la existencia de tal recta.

[Este problema es una nueva visión del problema 138 de la quincena del 1 al 15 de febrero de 2004, con una profundización]

Vicario, V. (2007): Comunicación personal.

Construcción de la bisectriz de un ángulo utilizando exclusivamente la regla.

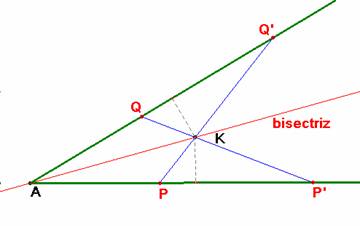Llevamos (con una regla) un segmento AP=AQ de longitud arbitraria, sobre cada lado. Repetimos la acción con otro segmento también arbitrario AP’= AQ’. Los segmentos PQ’ y P’Q se encuentran en el punto K, que está sobre la bisectriz del ángulo A como es fácil probar.

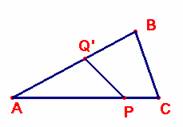La recta división pasa por el incentro

Según se explicó en el problema 138, si es APQ’ el triángulo cuya área es la mitad de la de ABC se verifica que: AP·AQ’ =bc/2  (1)

La igualdad de los perímetros supone AP + AQ’ = p   (2), donde p es el semiperímetro de ABC. En resumen: tenemos que construir dos segmentos AP  y AQ’ cuya suma y cuyo producto son dados. Ello equivale a resolver la ecuación

x² - px + bc/2 = 0      (3)

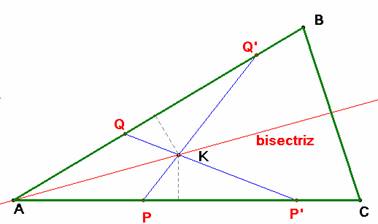
Una vez resuelta, llevando AP y AQ’ como se muestra en la figura se obtiene una recta solución, pero si el segmento AP se lleva sobre el lado AB y el AQ’ sobre el lado AC obtendremos otra recta solución. Los dos segmentos resultantes al hacer esta permutación se cortan, según lo dicho al comienzo en un punto K de la bisectriz de A. Concluiremos esta parte probando que K es el incentro del triángulo.

Supongamos que los puntos P, Q’; P’, Q son los extremos de los segmentos que realizan la división. Vamos a calcular el punto K. Tomamos el punto A como origen de los vectores y el lado AC como eje de abscisas. Para las rectas P’Q y PQ’ sus ecuaciones vectoriales son AX = AP + lPQ’ y AY = AP’ + l’P’Q respectivamente.

Para el punto común se tendrá la ecuación vectorial (con incógnitas l y l’)

AP’- AP= lPQ’ - l’P’Q

Sean P = (m,0) y P’=(n,0); el primer miembro de esa ecuación AP’- AP, es el vector (n – m ,0). Los otros puntos son Q = (m·cos A, m·sen A) y Q’= (n·cos A, n·sen A), de donde PQ’ = (n·cos A-m, n·sen A) y P’Q = (m·cos A-n, m·sen A), por tanto

lPQ’- l’P’Q = ((l n- l’m)·cos A- l m+l’ n, (ln- l’m)sen A)

La segunda coordenada es cero y la primera es n – m. Resulta que ln= l’m que nos permite suprimir l’ quedando , despejando queda . Sustituyendo este valor en la ecuación de la recta PQ’ se obtienen las coordenadas de K.

La segunda coordenada de este punto (del que sabemos que está sobre la bisectriz) es

y=, el radio del círculo inscrito, con lo cual queda probado que K es el incentro del triángulo (los segmentos m y n verifican las condiciones (1) y (2)).

Discusión

Las soluciones de la ecuación (3) son: 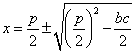(4)

Queremos estar seguros de que realmente existen al menos dos posibles divisiones del triángulo según deseamos. Si sustituimos el semiperímetro p, tendremos que el discriminante de esa ecuación es proporcional a (a+b+c)²-8bc. Siguiendo la línea del profesor García Capitán en el problema 138, podemos expresar

(a+b+c)²-8bc=(a+b- c)² +4c(a- b)=(a- b+c)² + 4b(a- c) (5)

Permutando los lados a, b y c, (para dividir el triángulo con segmentos opuestos a los ángulos B y C) se obtienen otras expresiones análogas para el discriminante de la correspondiente ecuación (4)

(a+b+c)²-8ac=(a- b- c)² +4a(b- c)=(a+b- c)² + 4c(b- a) (6)

(a+b+c)²-8ab=(a- b- c)² +4a(c- b)=(a- b+c)² + 4b(c- a) (7)

Si los lados del triángulo guardan entre sí una relación del tipo a ≤ b ≤ c, como las expresiones (a ± b ± c)² son positivas al tratarse de lados de un triángulo podemos asegurar que las expresiones (6) y (7) son positivas y por tanto que hay solución al problema.