Problema 404

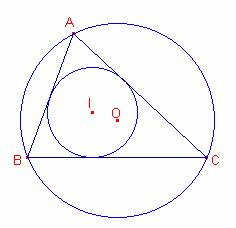Sean p, r, R el semiperímetro, radio del círculo inscrito y radio del círculo circunscrito al triángulo , respectivamente. Demostrar que: .

Solución de Ricard Peiró:

Del teorema d’Euler de la distancia entre el incentro y el circumcentro:

, entonces, la igualdad se alcanza cuando el triángulo es equilátero.

La circunferencia inscrita es interior al triángulo, entonces su perímetro es menor que el perímetro del triángulo, por tanto:

, entonces, la igualdad no se alcanza nunca.

Multiplicando las dos desigualdades:

.