Problema 406

Si dos rectas trazadas desde un vértice de un triángulo equilátero dividen el semicírculo exterior construido sobre el lado opuesto en tres arcos iguals, entonces estas rectas dividen dicho lado en tres segmentos iguales.

Coxeter (1994): "Retorno a la geometría" Editorial Euler. Colección la Tortuga de Aquiles. Madrid. (p. 26) Ejercicio 5

Si dos rectas trazadas desde un vértice de un triángulo equilátero dividen el semicírculo exterior construido sobre el lado opuesto en tres arcos iguals, entonces estas rectas dividen dicho lado en tres segmentos iguales.

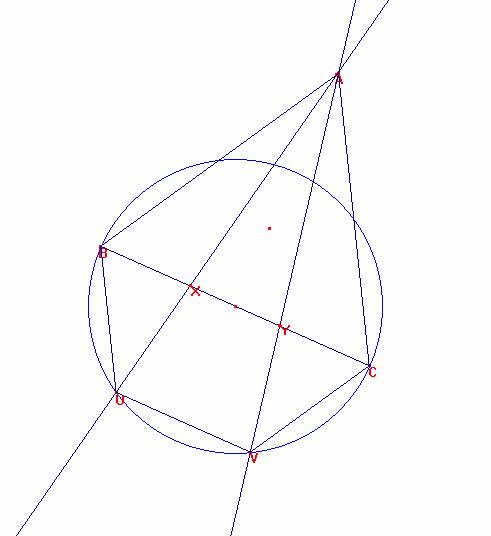
<BCV=<60º, <CBU=60º, por construcción de la circunferencia y las rectas.

1)  Los triángulos VYC y AYB son semejantes con

<YCV=<ABY=60º, y

<BYA=<VYC por opuestos por el vértice.

2.- Si A’ es el punto medio de BC, el triángulo A’VC es equilátero, pues A’C y A’V son radios, y al ser A’CV isósceles en A’ y medir <A’CV=60, es equilátero, cqd.

3) Luego CV mide a/2.

4) Al medir AB=a, tenemos que BY=2YC=2 x , por ser 2 la razón.

5) De igual modo procedemos con los triángulos BXU y AXC.

Así será XC=2BX=2y.

Tenemos que BY+2YC =BX+XC= BC = 3x=3y, luego x=y, cqd

Ricardo Barroso Campos

Didáctica de las Matemáticas.

Universidad de Sevilla