Problema 406

Si dos rectas trazadas desde un vértice de un triángulo equilátero dividen el semicírculo exterior construido sobre el lado opuesto en tres arcos iguals, entonces estas rectas dividen dicho lado en tres segmentos iguales

Coxeter “Retorno a la Geometría” página 26 ejercicio 5

Figura coxeterp26.fig

Applet created on 26/09/07 by User with CabriJava

Solución de Ricard Peiró:

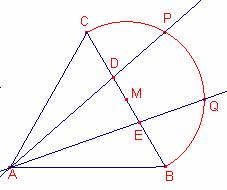Sea el triángulo equilátero , . Sea M el punto medio del lado .

Consideremos la semicircunferencia de diámetro , exterior al triángulo.

Sean P Q puntos de la semicircunferencia tal que dividen la semicircunferencia.

. Sea .

Aplicando el teorema del coseno al triángulo :

. .

.

, .

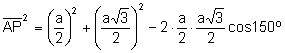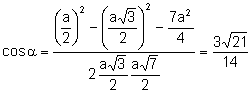Sea D la intersección de la recta AP y el lado , y E la intersección de la recta AQ y el lado .

Aplicando razones trigonométricas al triángulo rectángulo , :

.

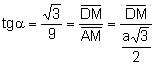Entonces, .

Análogamente, .

,

. .

Entonces las rectas AP, AQ dividen el lado en tres segmentos iguales.