Problema 406.- (Propuesto por Ricard Peiró i Estruch, I.E.S. “Abastos”, Valencia).

Si dos rectas trazadas desde un vértice de un triángulo equilátero dividen el semicírculo exterior construido sobre el lado opuesto en tres arcos iguales, entonces estas tres rectas dividen dicho lado en tres segmentos iguales.

Resolución: (Vicente Vicario García, Huelva)

            Aplicaremos la geometría analítica del plano para resolver el problema. Consideremos, sin pérdida de generalidad, un triángulo equilátero de lado 2 unidades. Usemos unos ejes cómodos de manera que el punto medio de la base del triángulo coincida con el eje de coordenadas y el mismo lado esté dispuesto sobre el eje de abscisas. Las coordenadas de los vértices del triángulo serán entonces como resultado de aplicar el teorema de Pitágoras, y .

            Consideremos ahora la semicircunferencia exterior (de radio unidad) dispuesta sobre el lado opuesto al vértice A.  Claramente la coordenadas de los puntos M y N que la trisecan son 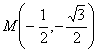 y 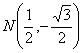. Determinemos la ecuación de la recta  que pasa por los puntos A y N. Para ello necesitamos un vector director  de la misma y uno de los dos puntos.

                         , 

            La ecuación de la recta es entonces

                                  

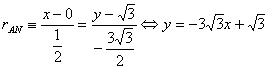
que corta al eje de abscisas en el punto . Claramente por simetría el otro punto de corte relativo a la segunda de las rectas trazadas  desde el vértice A será . Esto demuestra entonces que las rectas  y  trisecan el lado