Para el aula.

Propuesto por Ricard Peiró i Estruch Profesor de Matemáticas del IES "Abastos" (València)

Problema 406

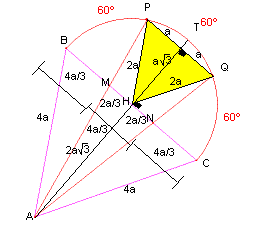
Si dos rectas trazadas desde un vértice de un triángulo equilátero dividen el semicírculo exterior construido sobre el lado opuesto en tres arcos iguales, entonces estas rectas dividen dicho lado en tres segmentos iguales.

Coxeter (1994) "Retorno a la geometría" Editorial Euler. Colección la Tortuga de Aquiles. Madrid. (p. 26). Ejercicio 5

SOLUCIÓN de William Rodríguez Chamache,. profesor de geometria de la "Academia integral class" Trujillo- Perú,:

Trazamos la altura AH que corta al arco PQ en T También observamos que PQ//BC y como los arcos miden 60º entonces el triángulo PHQ es equilátero Ahora sea la semicircunferencia de radio R=2.a entonces el triángulo ABC es de lado 4.a finalmente la altura AH= luego por semejanza obtenemos que y por lo tanto Finalmente por diferencia de segmento obtenemos que MB= y NC= De esto demostramos que: BM=MN=NC.