Problema 407

Sea un triángulo acutángulo ABC y sea P un punto interior al mismo. Sean los ángulos , , .  Caracterizar el punto P de manera que la suma  sea mínima.

Resolución: (Vicente Vicario García, Huelva)

Obviamente tenemos que . Utilicemos ahora relaciones trigonométricas básicas y fórmulas de transformación de sumas en productos para determinar la siguiente expresión

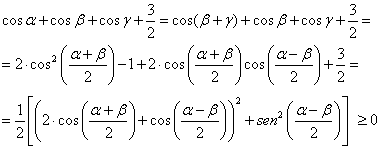
de  la que se deduce

            El punto P donde se alcanza el valor mínimo es aquel en el que se tiene la igualdad, es decir, , Es conocido que P es el denominado primer punto  de Fermat (o punto de Torricelli, o punto de Steiner, según versiones) del triángulo, que es el punto que minimiza la suma de distancias a los vértices del mismo. Además, el punto de minimización sigue teniendo esta misma caracterización siempre que el mayor de los ángulos del triángulo sea menor de 120º. Si el mayor ángulo del triángulo es superior o igual a 120º el punto que minimiza la suma de distancias a los vértices coincide con el vértice de este ángulo. Pero independientemente del valor del mayor ángulo del triángulo, la solución de nuestro problema sigue siendo válida, aunque el punto P se encuentre en el exterior del triángulo (segundo punto de Fermat ). La construcción de los puntos de Fermat es muy conocida y sencilla a partir de triángulos equiláteros construidos hacia el exterior e interior de los lados del triángulo dado.