Problema 408
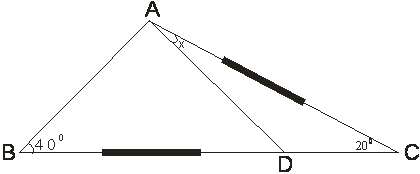
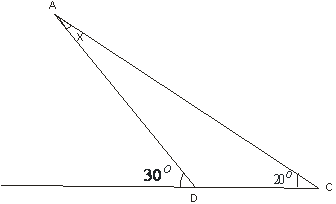
En el triángulo ABC, B=40º, C=20º, D en BC, BD=AC. Hallar <DAC.
Salazar, J. C. (2004): Comunicación personal.
Solución de Alejandro Cipriano Coronel,estudiante de ingeniería de
De acuerdo al problema el diseño sería aproximadamente como sigue:
Se prolonga CB hasta un punto P tal que: AB=BP y se construye el triángulo isósceles ABP
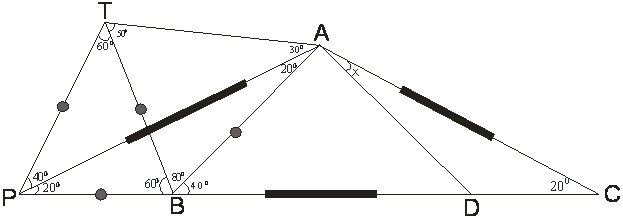
Luego en BP se construye el triángulo equilátero PTB y se une los puntos T y A generando un triángulo isósceles (ABT): m< BTA = m< BAT = 50º pero m< BAP = 20º; entonces
m< PAT = 30º.
Además en el triángulo TPA es congruente al triángulo ABD (caso: Ángulo, Lado, Ángulo)
O sea: TP = AB, AP = BD, m< TPA = m< ABD = 40º; entonces: m< PAT = m< ADB
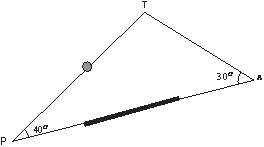
![]()
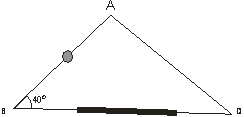
Por lo tanto la m< PAT = m< ADB = 30º
Y finalmente en el triángulo ADC por ángulo exterior se tiene que: 20º + X = 30º
Y de ahí se tiene que: X = 10º … RPTA.